Franklin system

One of the classical orthonormal systems of continuous functions. The Franklin system 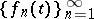(see [1] or [2]) is obtained by applying the Schmidt orthogonalization process (cf. Orthogonalization method) on the interval 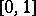to the Faber–Schauder system, which is constructed using the set of all dyadic rational points in 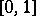; in this case the Faber–Schauder system is, up to constant multiples, the same as the system 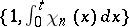, where 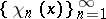is the Haar system. The Franklin system was historically the first example of a basis in the space of continuous functions that had the property of orthogonality. This system is also a basis in all the spaces 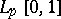, 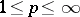(see [3]). If a continuous function 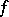on has modulus of continuity 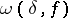, and 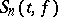is the partial sum of order of the Fourier series of 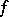with respect to the Franklin system, then

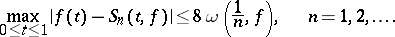Here the Fourier–Franklin coefficients 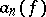of 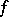satisfy the inequalities

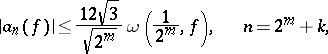and the conditions

a) , ;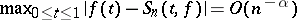

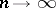b) , ;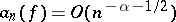

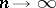c) 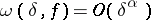, 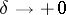; are equivalent for .

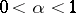If the continuous function is such that

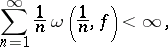then the series

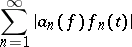converges uniformly on 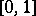, and if

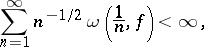then

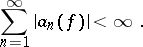All these properties of the Franklin system are proved by using the inequalities

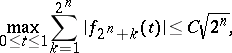The Franklin system is an unconditional basis in all the spaces 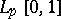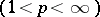and, moreover, in all reflexive Orlicz spaces (see [5]). If 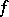belongs to 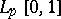, , 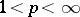then one has the inequality

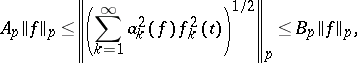where 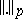denotes the norm in 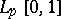, and the constants 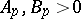depend only on .

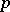The Franklin system has had important applications in various questions in analysis. In particular, bases in the spaces 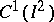(see [4]) and 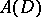(see [5]) have been constructed using this system. Here 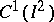is the space of all continuously-differentiable functions 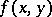on the square 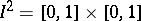with the norm

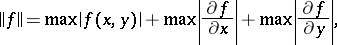and 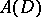, the disc space, is the space of all functions 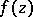that are analytic in the open disc 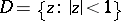in the complex plane and continuous in the closed disc 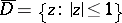with the norm

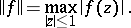The questions of whether there are bases in 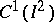and 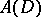were posed by S. Banach [6].

References

[1]	P. Franklin, "A set of continuous orthogonal functions" Math. Ann. , 100 (1928) pp. 522–529
[2]	S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951)
[3]	Z. Ciesielski, "Properties of the orthogonal Franklin system" Studia Math. , 23 : 2 (1963) pp. 141–157
[4]	Z. Ciesielski, "A construction of a basis in 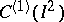" Studia Math. , 33 : 2 (1969) pp. 243–247
[5]	S.V. Bochkarev, "Existence of a basis in the space of functions analytic in the disk, and some properties of Franklin's system" Math. USSR-Sb. , 24 : 1 (1974) pp. 1–16 Mat. Sb. , 95 : 1 (1974) pp. 3–18
[6]	S.S. Banach, "Théorie des opérations linéaires" , Chelsea, reprint (1955)