Alternating group

of degree

The subgroup of the symmetric group consisting of all even permutations. is a normal subgroup in of index 2 and order . The permutations of , considered as permutations of the indices of variables , leave the alternating polynomial invariant, hence the term "alternating group" . The group may also be defined for infinite cardinal numbers 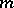, as the subgroup of 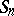consisting of all even permutations. If , the group 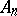is 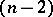-fold transitive. For any , finite or infinite, except , this group is simple; this fact plays an important role in the theory of solvability of algebraic equations by radicals.

References

[1]	M. Hall, "Group theory" , Macmillan (1959)

Comments

Note that 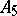is the non-Abelian simple group of smallest possible order.