Integral cosine
The special function defined, for real 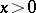 , by
, by
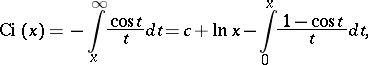 |
where  is the Euler constant. Its graph is:
is the Euler constant. Its graph is:
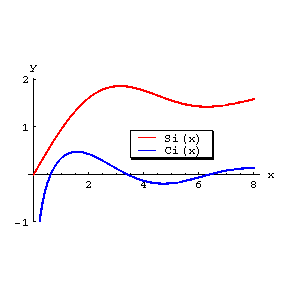
Figure: i051370a
The graphs of the functions 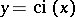 and
and 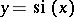 .
.
Some integrals related to the integral cosine are:
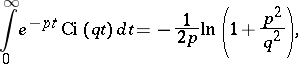 |
 |
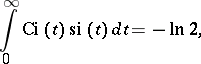 |
where 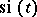 is the integral sine minus
is the integral sine minus 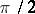 .
.
For  small:
small:
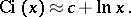 |
The asymptotic representation, for  large, is:
large, is:
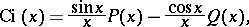 |
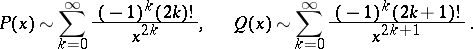 |
The integral cosine has the series representation:
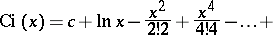 | (*) |
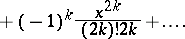 |
As a function of the complex variable  ,
, 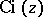 , defined by (*), is a single-valued analytic function in the
, defined by (*), is a single-valued analytic function in the  -plane with slit along the relative negative real axis
-plane with slit along the relative negative real axis 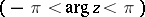 . The value of
. The value of 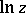 here is taken to be
here is taken to be 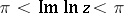 . The behaviour of
. The behaviour of 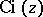 near the slit is determined by the limits
near the slit is determined by the limits
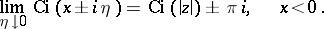 |
The integral cosine is related to the integral exponential function 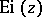 by
by
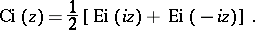 |
One sometimes uses the notation 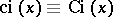 .
.
See also Si-ci-spiral.
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
| [3] | A. Kratzer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
| [4] | N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian) |
Comments
The function 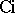 is better known as the cosine integral. It can, of course, be defined by the integral (as above) in
is better known as the cosine integral. It can, of course, be defined by the integral (as above) in 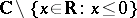 .
.
Integral cosine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_cosine&oldid=16619