Abstract Witt ring
There are many definitions of an abstract Witt ring. They all seek to define a class of rings that includes Witt rings of fields (of characteristic not two) and that is closed under fibre products, extensions by groups of exponent two and certain quotients. The need for such a class of rings became apparent early in the (still incomplete) classification of Noetherian Witt rings of fields.
Two series of definitions, that of J. Kleinstein and A. Rosenberg [a1] and M. Marshall [a2], led to the same class of rings, which is now the most widely used. In this sense, an abstract Witt ring is a pair 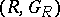 where
where 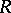 is a commutative ring with unit
is a commutative ring with unit 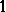 and
and  is a subgroup of the multiplicative group
is a subgroup of the multiplicative group 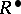 which has exponent two, contains
which has exponent two, contains  and generates
and generates 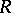 additively. Let
additively. Let  denote the ideal of
denote the ideal of  generated by elements of the form
generated by elements of the form 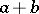 , with
, with 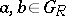 . It is further assumed that:
. It is further assumed that:
1) if 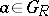 , then
, then  ;
;
2) if 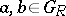 and
and 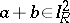 , then
, then 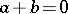 ;
;
3) if 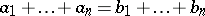 , with
, with 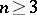 and all
and all 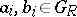 , then there exist
, then there exist  such that
such that 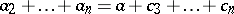 and
and 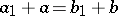 .
.
When 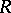 is the Witt ring of a field
is the Witt ring of a field 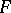 , then
, then 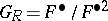 and property 3) is a consequence of the Witt cancellation theorem.
and property 3) is a consequence of the Witt cancellation theorem.
References
| [a1] | J. Kleinstein, A. Rosenberg, "Succinct and representational Witt rings" Pacific J. Math. , 86 (1980) pp. 99 – 137 |
| [a2] | M. Marshall, "Abstract Witt rings" , Queen's Univ. (1980) |
Abstract Witt ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abstract_Witt_ring&oldid=16610