Coset in a group
by a subgroup 
(from the left)
A set of elements of 
of the form
 |
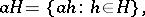where 
is some fixed element of 
. This coset is also called the left coset by 
in 
defined by 
. Every left coset is determined by any of its elements. 
if and only if 
. For all 
the cosets 
and 
are either equal or disjoint. Thus, 
decomposes into pairwise disjoint left cosets by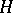 
; this decomposition is called the left decomposition of 
with respect to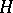 
. Similarly one defines right cosets (as sets 
, 
) and also the right decomposition of 
with respect to 
. These decompositions consist of the same number of cosets (in the infinite case, their cardinalities are equal). This number (cardinality) is called the index of the subgroup 
in 
. For normal subgroups, the left and right decompositions coincide, and in this case one simply speaks of the decomposition of a group with respect to a normal subgroup.
Comments
See also Normal subgroup.
Coset in a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coset_in_a_group&oldid=16601