Legendre manifold
An  -dimensional smooth submanifold
-dimensional smooth submanifold 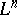 of a
of a  -dimensional contact manifold
-dimensional contact manifold 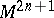 (that is, a manifold endowed with a Pfaffian form
(that is, a manifold endowed with a Pfaffian form  such that the exterior product of it with the
such that the exterior product of it with the  -th exterior power of its exterior differential
-th exterior power of its exterior differential 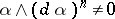 at all points of
at all points of 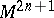 ), such that the Pfaffian form
), such that the Pfaffian form 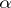 that specifies the contact structure on
that specifies the contact structure on 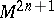 vanishes identically on
vanishes identically on 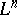 (that is,
(that is, 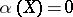 for any vector
for any vector  that is tangent to
that is tangent to 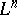 at some point of
at some point of 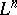 ). In the important special case when
). In the important special case when  with coordinates
with coordinates 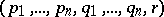 ,
, 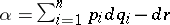 and
and 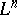 is situated so that the
is situated so that the 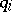 can be taken as coordinates on it, the condition that
can be taken as coordinates on it, the condition that 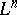 is a Legendre manifold means that it is specified by equations of the form
is a Legendre manifold means that it is specified by equations of the form
 |
If the 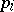 can also be taken as coordinates on
can also be taken as coordinates on 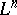 , then the coordinates
, then the coordinates 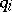 and
and 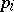 are connected by a Legendre transformation (cf. Legendre transform); if this cannot be done in a neighbourhood of some point, then the Legendre transformation has a singularity at this point.
are connected by a Legendre transformation (cf. Legendre transform); if this cannot be done in a neighbourhood of some point, then the Legendre transformation has a singularity at this point.
Examples of Legendre manifolds occurred long ago in various questions of analysis and geometry, but the idea of the Legendre manifold itself was introduced comparatively recently by analogy with a Lagrangian manifold.
References
| [1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [2] | V.I. [V.I. Arnol'd] Arnold, A.B. [A.B. Givent'al] Giventhal, "Symplectic geometry" , Dynamical Systems , IV , Springer (1989) pp. Chapt. 4 (Translated from Russian) |
Comments
The generalization of solutions of first-order partial differential equations to Legendre manifolds is due to S. Lie, see [a1], §23, 26, although Lie did not give a name to it.
References
| [a1] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1 , Birkhäuser (1985) pp. Chapt. 20 (Translated from Russian) |
| [a2] | S. Lie, F. Engel, "Theorie der Transformationsgruppen" , II , Leipzig (1930) |
Legendre manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Legendre_manifold&oldid=16584