Implicit operator
A solution 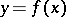 of a non-linear operator equation
of a non-linear operator equation 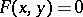 , in which
, in which  plays the role of parameter and
plays the role of parameter and 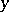 that of the unknown. Let
that of the unknown. Let 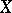 ,
, 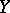 and
and 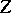 be Banach spaces and let
be Banach spaces and let  be a non-linear operator that is continuous in a neighbourhood
be a non-linear operator that is continuous in a neighbourhood  of
of 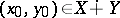 and that maps
and that maps  into a neighbourhood of zero in
into a neighbourhood of zero in 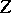 . If the Fréchet derivative
. If the Fréchet derivative  is continuous on
is continuous on  , if the operator
, if the operator 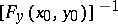 exists and is continuous and if
exists and is continuous and if 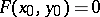 , then there are numbers
, then there are numbers 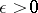 and
and 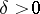 such that for
such that for 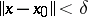 the equation
the equation 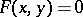 has a unique solution
has a unique solution 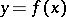 in the ball
in the ball 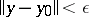 . Here if, additionally,
. Here if, additionally, 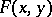 is
is  times differentiable in
times differentiable in  , then
, then 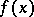 is
is  times differentiable. If
times differentiable. If  is an analytic operator in
is an analytic operator in  , then
, then 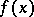 is also analytic. These assertions generalize well-known propositions about implicit functions. For degenerate cases, see Branching of solutions of non-linear equations.
is also analytic. These assertions generalize well-known propositions about implicit functions. For degenerate cases, see Branching of solutions of non-linear equations.
References
| [1] | T.H. Hildebrandt, L.M. Graves, "Implicit functions and their differences in general analysis" Trans. Amer. Math. Soc. , 29 (1927) pp. 127–153 |
| [2] | W.I. [V.I. Sobolev] Sobolew, "Elemente der Funktionalanalysis" , H. Deutsch , Frankfurt a.M. (1979) (Translated from Russian) |
| [3] | M.M. Vainberg, V.A. Trenogin, "Theory of branching of solutions of non-linear equations" , Noordhoff (1974) (Translated from Russian) |
| [4] | L. Nirenberg, "Topics in nonlinear functional analysis" , New York Univ. Inst. Math. Mech. (1974) |
Comments
References
| [a1] | M.S. Berger, "Nonlinearity and functional analysis" , Acad. Press (1977) |
Implicit operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Implicit_operator&oldid=16566