Farey series
From Encyclopedia of Mathematics
of order 
The increasing sequence of non-negative irreducible fractions not exceeding 1 with denominators not exceeding  . For example, the Farey series of order 5 is the sequence
. For example, the Farey series of order 5 is the sequence
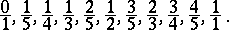 |
The following assertions hold.
1) If 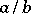 and
and 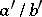 are two consecutive terms of the Farey series of order
are two consecutive terms of the Farey series of order  , then
, then
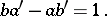 |
2) If 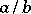 ,
, 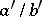 ,
, 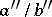 are three consecutive terms of the Farey series of order
are three consecutive terms of the Farey series of order  , then
, then
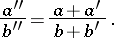 |
3) The number of terms in the Farey series of order  is equal to
is equal to
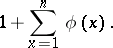 | (*) |
Farey series were investigated by J. Farey (1816).
References
| [1] | A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian) |
| [2] | R.R. Hall, "A note on Farey series" J. London Math. Soc. , 2 (1970) pp. 139–148 |
| [3] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) |
Comments
Of course, in (*) 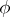 denotes the Euler function.
denotes the Euler function.
How to Cite This Entry:
Farey series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Farey_series&oldid=16556
Farey series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Farey_series&oldid=16556
This article was adapted from an original article by V.I. Nechaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article