Rosinger nowhere-dense generalized function algebra
In the general framework of generalized function algebras developed by E.E. Rosinger [a3], [a4], [a5], [a6], a distinguished role is played by ideals in the sequence algebra 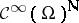 ,
,  an open subset of
an open subset of  , which are defined by vanishing properties. Given a family
, which are defined by vanishing properties. Given a family  of subsets of
of subsets of  , stable under finite unions, one considers the ideal
, stable under finite unions, one considers the ideal 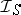 in
in 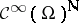 determined by those
determined by those  for which there is a
for which there is a 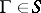 such that for all
such that for all  ,
, 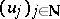 vanishes near
vanishes near  eventually, that is, there are a
eventually, that is, there are a 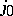 and a neighbourhood
and a neighbourhood 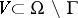 of
of  such that
such that 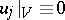 for
for  . The nowhere-dense generalized function algebra
. The nowhere-dense generalized function algebra 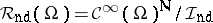 is obtained when
is obtained when 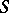 is the class of nowhere-dense, closed subsets of
is the class of nowhere-dense, closed subsets of  . The space
. The space 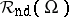 contains
contains  via the constant imbedding. It has two distinguishing features. First, the family
via the constant imbedding. It has two distinguishing features. First, the family 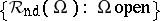 forms a flabby sheaf, and in a certain sense the smallest flabby sheaf containing
forms a flabby sheaf, and in a certain sense the smallest flabby sheaf containing 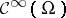 , see [a2]. Secondly, the algebra
, see [a2]. Secondly, the algebra  of (equivalence classes of) smooth functions defined off some nowhere-dense, closed subset of
of (equivalence classes of) smooth functions defined off some nowhere-dense, closed subset of  can be imbedded into
can be imbedded into  .
.
In particular, solutions to partial differential equations defined piecewise off nowhere-dense closed sets 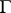 (no growth restrictions near
(no growth restrictions near 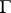 ) can be interpreted as global solutions in
) can be interpreted as global solutions in  by means of a suitable regularization method. The space of distributions
by means of a suitable regularization method. The space of distributions 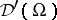 (cf. also Generalized functions, space of) is imbedded in any algebra of the form
(cf. also Generalized functions, space of) is imbedded in any algebra of the form 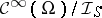 by a general procedure [a4] using an algebraic basis.
by a general procedure [a4] using an algebraic basis.
Further generalizations of the ideal 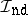 to include larger exceptional sets as well as applications to non-smooth differential geometry can be found in [a1]; non-linear Lie group actions on generalized functions using the framework of
to include larger exceptional sets as well as applications to non-smooth differential geometry can be found in [a1]; non-linear Lie group actions on generalized functions using the framework of 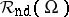 are studied in [a7].
are studied in [a7].
Replacing the single differential algebra 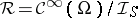 with chains of algebras
with chains of algebras 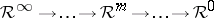 using the spaces
using the spaces 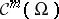 in the place of
in the place of 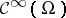 at each level, allows one to achieve consistency of the multiplication and derivation with the pointwise product of
at each level, allows one to achieve consistency of the multiplication and derivation with the pointwise product of 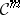 -functions as well as the derivative of
-functions as well as the derivative of 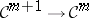 at each fixed level
at each fixed level  .
.
See also Generalized function algebras.
References
| [a1] | A. Mallios, E.E. Rosinger, "Space-time foam dense singularities and de Rham cohomology" Acta Applic. Math. (to appear) |
| [a2] | M. Oberguggenberger, E.E. Rosinger, "Solution of continuous nonlinear PDEs through order completion" , North-Holland (1994) |
| [a3] | E.E. Rosinger, "Distributions and nonlinear partial differential equations" , Springer (1978) |
| [a4] | E.E. Rosinger, "Nonlinear partial differential equations. Sequential and weak solutions" , North-Holland (1980) |
| [a5] | E.E. Rosinger, "Generalized solutions of nonlinear partial differential equations" , North-Holland (1987) |
| [a6] | E.E. Rosinger, "Nonlinear partial differential equations, an algebraic view of generalized solutions" , North-Holland (1990) |
| [a7] | E.E. Rosinger, "Parametric Lie group actions on global generalized solutions of nonlinear PDEs. Including a solution to Hilbert's fifth problem" , Kluwer Acad. Publ. (1998) |
Rosinger nowhere-dense generalized function algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rosinger_nowhere-dense_generalized_function_algebra&oldid=16555