Tits quadratic form

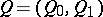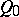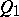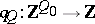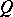Let be a finite quiver (see [a8]), that is, an oriented graph with vertex set and set of arrows (oriented edges; cf. also Graph, oriented; Quiver). Following P. Gabriel [a8], [a9], the Tits quadratic form of is defined by the formula

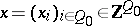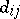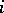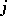where and is the number of arrows from to in .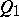

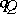There are important applications of the Tits form in representation theory. One easily proves that if is connected, then is positive definite if and only if 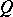(viewed as a non-oriented graph) is any of the Dynkin diagrams 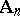, , 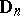, , 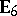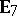or 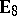(cf. also Dynkin diagram). On the other hand, the Gabriel theorem [a8] asserts that this is the case if and only if 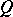has only finitely many isomorphism classes of indecomposable 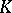-linear representations, where 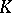is an algebraically closed field (see also [a2]). Let 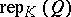be the Abelian category of finite-dimensional 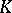-linear representations of 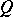formed by the systems 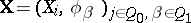of finite-dimensional vector 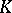-spaces 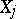, connected by 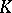-linear mappings 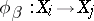corresponding to arrows 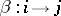of 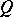. By a theorem of L.A. Nazarova [a12], given a connected quiver 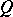the category 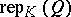is of tame representation type (see [a7], [a10], [a19] and Quiver) if and only if 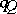is positive semi-definite, or equivalently, if and only if 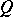(viewed as a non-oriented graph) is any of the extended Dynkin diagrams , , 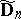, , 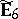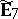or (see [a1], [a10], [a19]; and [a4] for a generalization).

Let 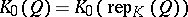be the Grothendieck group of the category 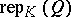. By the Jordan–Hölder theorem, the correspondence 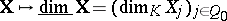defines a group isomorphism 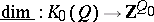. One shows that the Tits form 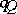coincides with the Euler characteristic 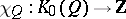, , 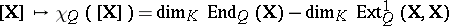along the isomorphism 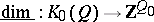, that is, 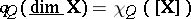for any 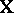in (see [a10], [a17]).

The Tits quadratic form 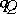is related with an algebraic geometry context defined as follows (see [a9], [a10], [a19]).

For any vector 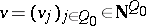, consider the affine irreducible 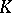-variety 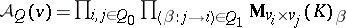of 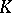-representations of 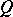of the dimension type (in the Zariski topology), where 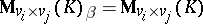is the space of 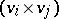-matrices for any arrow 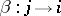of 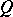. Consider the algebraic group 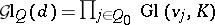and the algebraic group action 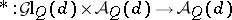defined by the formula 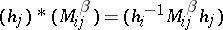, where 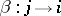is an arrow of 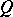, , 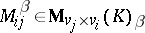, and 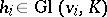. An important role in applications is played by the Tits-type equality 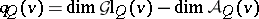, , 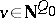where denotes the dimension of the algebraic variety (see [a8]).

Following the above ideas, Yu.A. Drozd [a5] introduced and successfully applied a Tits quadratic form in the study of finite representation type of the Krull–Schmidt category 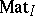of matrix 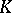-representations of partially ordered sets 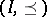with a unique maximal element (see [a10], [a19]). In [a6] and [a7] he also studied bimodule matrix problems and the representation type of boxes 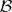by means of an associated Tits quadratic form 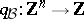(see also [a18]). In particular, he showed [a6] that if 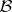is of tame representation type, then 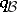is weakly non-negative, that is, 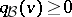for all .

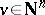K. Bongartz [a3] associated with any finite-dimensional basic 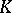-algebra 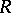a Tits quadratic form as follows. Let 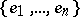be a complete set of primitive pairwise non-isomorphic orthogonal idempotents of the algebra 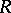. Fix a finite quiver 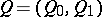with 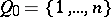and a 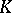-algebra isomorphism 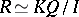, where 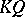is the path 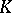-algebra of the quiver 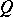(see [a1], [a10], [a19]) and 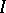is an ideal of 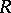contained in the square of the Jacobson radical 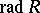of 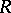and containing a power of 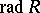. Assume that 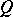has no oriented cycles (and hence the global dimension of 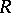is finite). The Tits quadratic form 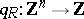of 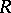is defined by the formula

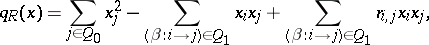where 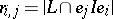, for a minimal set 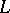of generators of 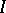contained in 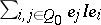. One checks that 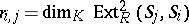, where 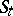is the simple 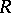-module associated to the vertex 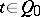. Then the definition of 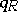depends only on 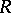, and when 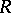is of global dimension at most two, the form 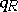coincides with the Euler characteristic 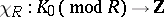, , 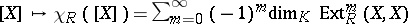under a group isomorphism 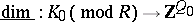, where 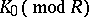is the Grothendieck group of the category 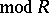of finite-dimensional right 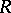-modules (see [a17]). Note that if .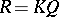

By applying a Tits-type equality as above, Bongartz [a3] proved that if 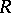is of finite representation type, then 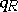is weakly positive, that is, 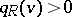for all non-zero vectors 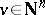. The converse implication does not hold in general, but it has been established if the Auslander–Reiten quiver of 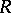(see Riedtmann classification) has a post-projective component (see [a10]), by applying an idea of Drozd [a5]. J.A. de la Peña [a14] proved that if 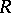is of tame representation type, then 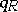is weakly non-negative. The converse implication does not hold in general, but it has been proved under a suitable assumption on 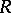(see [a13] and [a16] for a discussion of this problem and relations between the Tits quadratic form and the Euler quadratic form of ).

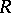Let 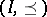be a partially ordered set with partial order relation 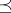and let 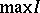be the set of all maximal elements of 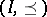. Following [a5] and [a15], D. Simson [a20] defined the Tits quadratic form 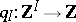of 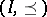by the formula

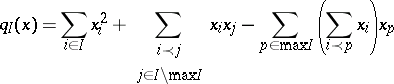and applied it in the study of prinjective 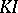-modules, that is, finite-dimensional right modules 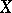over the incidence 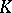-algebra 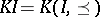of 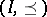such that there is an exact sequence 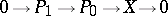, where 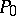is a projective 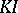-module and 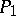is a direct sum of simple projectives. The additive Krull–Schmidt category 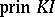of prinjective 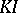-modules is equivalent to the category of matrix 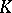-representations of 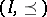[a20]. Under an identification 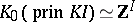, the Tits form 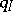is equal to the Euler characteristic 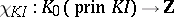. A Tits-type equality is also valid for 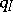[a15]. It has been proved in [a20] that 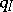is weakly positive if and only if 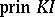has only a finite number of iso-classes of indecomposable modules. By [a15], if 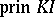is of tame representation type, then 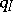is weakly non-negative. The converse implication does not hold in general, but it has been proved under some assumption on 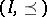(see [a11]).

A Tits quadratic form 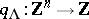for a class of classical 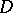-orders 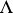, where 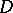is a complete discrete valuation domain, has been defined in [a21]. Criteria for the finite lattice type and tame lattice type of 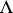are given in [a21] by means of .

For a class of 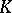-co-algebras , a Tits quadratic form is defined in [a22], and the co-module types of 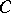are studied by means of 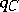, where 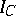is a complete set of pairwise non-isomorphic simple left 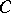-co-modules and 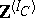is a free Abelian group of rank .

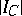References

[a1]	V.I. Auslander, I. Reiten, S. Smalø, "Representation theory of Artin algebras" , Studies Adv. Math. , 36 , Cambridge Univ. Press (1995)
[a2]	I.N. Bernstein, I.M. Gelfand, V.A. Ponomarev, "Coxeter functors and Gabriel's theorem" Russian Math. Surveys , 28 (1973) pp. 17–32 Uspekhi Mat. Nauk. , 28 (1973) pp. 19–33
[a3]	K. Bongartz, "Algebras and quadratic forms" J. London Math. Soc. , 28 (1983) pp. 461–469
[a4]	V. Dlab, C.M. Ringel, "Indecomposable representations of graphs and algebras" , Memoirs , 173 , Amer. Math. Soc. (1976)
[a5]	Yu.A. Drozd, "Coxeter transformations and representations of partially ordered sets" Funkts. Anal. Prilozhen. , 8 (1974) pp. 34–42 (In Russian)
[a6]	Yu.A. Drozd, "On tame and wild matrix problems" , Matrix Problems , Akad. Nauk. Ukr. SSR., Inst. Mat. Kiev (1977) pp. 104–114 (In Russian)
[a7]	Yu.A. Drozd, "Tame and wild matrix problems" , Representations and Quadratic Forms (1979) pp. 39–74 (In Russian)
[a8]	P. Gabriel, "Unzerlegbare Darstellungen 1" Manuscripta Math. , 6 (1972) pp. 71–103 (Also: Berichtigungen 6 (1972), 309)
[a9]	P. Gabriel, "Représentations indécomposables" , Séminaire Bourbaki (1973/74) , Lecture Notes in Mathematics , 431 , Springer (1975) pp. 143–169
[a10]	P. Gabriel, A.V. Roiter, "Representations of finite dimensional algebras" , Algebra VIII , Encycl. Math. Stud. , 73 , Springer (1992)
[a11]	S. Kasjan, D. Simson, "Tame prinjective type and Tits form of two-peak posets II" J. Algebra , 187 (1997) pp. 71–96
[a12]	L.A. Nazarova, "Representations of quivers of infinite type" Izv. Akad. Nauk. SSSR , 37 (1973) pp. 752–791 (In Russian)
[a13]	J.A. de la Peña, "Algebras with hypercritical Tits form" , Topics in Algebra , Banach Center Publ. , 26: 1 , PWN (1990) pp. 353–369
[a14]	J.A. de la Peña, "On the dimension of the module-varieties of tame and wild algebras" Commun. Algebra , 19 (1991) pp. 1795–1807
[a15]	J.A. de la Peña, D. Simson, "Prinjective modules, reflection functors, quadratic forms and Auslander–Reiten sequences" Trans. Amer. Math. Soc. , 329 (1992) pp. 733–753
[a16]	J.A. de la Peña, A. Skowroński, "The Euler and Tits forms of a tame algebra" Math. Ann. , 315 (2000) pp. 37–59
[a17]	C.M. Ringel, "Tame algebras and integral quadratic forms" , Lecture Notes in Mathematics , 1099 , Springer (1984)
[a18]	A.V. Roiter, M.M. Kleiner, "Representations of differential graded categories" , Lecture Notes in Mathematics , 488 , Springer (1975) pp. 316–339
[a19]	D. Simson, "Linear representations of partially ordered sets and vector space categories" , Algebra, Logic Appl. , 4 , Gordon & Breach (1992)
[a20]	D. Simson, "Posets of finite prinjective type and a class of orders" J. Pure Appl. Algebra , 90 (1993) pp. 77–103
[a21]	D. Simson, "Representation types, Tits reduced quadratic forms and orbit problems for lattices over orders" Contemp. Math. , 229 (1998) pp. 307–342
[a22]	D. Simson, "Coalgebras, comodules, pseudocompact algebras and tame comodule type" Colloq. Math. , in press (2001)