Commutant lifting theorem
Let 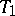 be a contraction on a Hilbert space
be a contraction on a Hilbert space 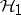 , that is,
, that is, 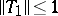 . Recall that
. Recall that 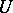 is an isometric dilation of
is an isometric dilation of 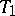 if
if 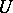 is an isometry (cf. Isometric operator) on a Hilbert space
is an isometry (cf. Isometric operator) on a Hilbert space 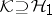 and
and 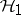 is an invariant subspace for
is an invariant subspace for 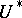 satisfying
satisfying 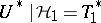 . The Sz.-Nagy–Shäffer construction shows that all contractions admit an isometric dilation [a1], [a5]. This sets the stage for the following result, known as the Sz.-Nagy–Foias commutant lifting theorem [a1], [a4], [a5].
. The Sz.-Nagy–Shäffer construction shows that all contractions admit an isometric dilation [a1], [a5]. This sets the stage for the following result, known as the Sz.-Nagy–Foias commutant lifting theorem [a1], [a4], [a5].
Let 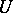 on
on 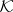 be an isometric dilation for a contraction
be an isometric dilation for a contraction 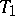 on
on 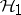 . Let
. Let 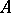 be an operator from the Hilbert space
be an operator from the Hilbert space 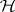 into
into 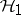 and
and 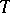 an isometry on
an isometry on 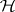 satisfying
satisfying 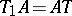 . Then there exists an operator
. Then there exists an operator 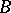 from
from 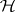 into
into 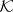 satisfying the following three conditions:
satisfying the following three conditions: 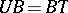 ,
, 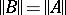 and
and 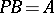 , where
, where 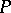 is the orthogonal projection onto
is the orthogonal projection onto 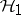 .
.
The commutant lifting theorem was inspired by seminal work of D. Sarason [a3] on 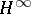 interpolation. It can be used to solve many classical and modern
interpolation. It can be used to solve many classical and modern 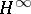 interpolation problems, including the Carathéodory, Nevanlinna–Pick, Hermite–Féjer, Nudelman, Nehari, and Löwner interpolation problems in both their classical and tangential form (see [a1] and also Carathéodory interpolation; Nevanlinna–Pick interpolation). The commutant lifting theorem can also be used to solve problems in
interpolation problems, including the Carathéodory, Nevanlinna–Pick, Hermite–Féjer, Nudelman, Nehari, and Löwner interpolation problems in both their classical and tangential form (see [a1] and also Carathéodory interpolation; Nevanlinna–Pick interpolation). The commutant lifting theorem can also be used to solve problems in 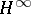 control theory and inverse scattering [a1], [a2].
control theory and inverse scattering [a1], [a2].
There is a one-to-one correspondence between the set of all solutions in the commutant lifting theorem and a certain choice sequence of contractions. This choice sequence is a generalization of the Schur numbers used to solve the Carathéodory interpolation problem or the reflection coefficients appearing in inverse scattering problems for layered media in geophysics. There is also a one-to-one correspondence between the sets of all solutions for the commutant lifting theorem and a certain contractive analytic function in the open unit disc. This characterization of all solutions has several different network interpretations [a1].
As an illustration of the commutant lifting theorem, consider the Nehari interpolation problem
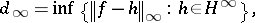 |
where  is a given function in
is a given function in 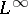 . Here,
. Here, 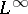 is the Banach space of all Lebesgue-measurable functions
is the Banach space of all Lebesgue-measurable functions 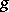 on the unit circle whose norm
on the unit circle whose norm 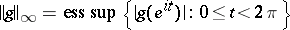 is finite, and
is finite, and 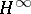 is the subspace of
is the subspace of 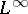 consisting of all functions
consisting of all functions 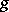 in
in 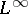 whose Fourier coefficients at
whose Fourier coefficients at 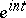 are zero for all
are zero for all 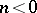 . Likewise,
. Likewise, 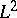 is the Hilbert space of all Lebesgue-measurable, square-integrable functions on the unit circle, and
is the Hilbert space of all Lebesgue-measurable, square-integrable functions on the unit circle, and 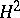 is the subspace of
is the subspace of 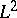 consisting of all functions in
consisting of all functions in 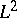 whose Fourier coefficients at
whose Fourier coefficients at 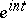 vanish for all
vanish for all 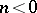 . Now, let
. Now, let 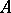 be the Hankel operator from
be the Hankel operator from 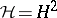 into
into 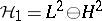 defined by
defined by 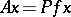 for
for  in
in 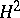 . Let
. Let 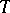 be the isometry on
be the isometry on 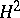 and
and 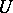 the unitary operator on
the unitary operator on 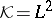 defined by
defined by 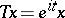 and
and 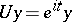 , respectively. Let
, respectively. Let 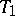 be the contraction on
be the contraction on 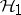 defined by
defined by  for
for 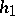 in
in 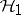 . Since
. Since 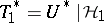 , it follows that
, it follows that 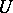 is an isometric lifting of
is an isometric lifting of 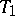 . By applying the commutant lifting theorem, there exists an operator
. By applying the commutant lifting theorem, there exists an operator 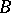 from
from 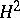 into
into 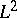 satisfying
satisfying 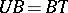 ,
, 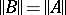 and
and 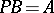 . Therefore, the error
. Therefore, the error  , and there exists an
, and there exists an 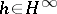 such that
such that 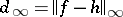 .
.
References
| [a1] | C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , Operator Theory: Advances and Applications , 44 , Birkhäuser (1990) |
| [a2] | C. Foias, H. Özbay, A. Tannenbaum, "Robust control of infinite-dimensional systems" , Springer (1996) |
| [a3] | D. Sarason, "Generalized interpolation in 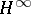 " Trans. Amer. Math. Soc. , 127 (1967) pp. 179–203 " Trans. Amer. Math. Soc. , 127 (1967) pp. 179–203 |
| [a4] | B. Sz.-Nagy, C. Foias, "Dilatation des commutants d'opérateurs" C.R. Acad. Sci. Paris , A266 (1968) pp. 493–495 |
| [a5] | B. Sz.-Nagy, C. Foias, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) |
Commutant lifting theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Commutant_lifting_theorem&oldid=16540