Polynomial function
A generalization of the concept of an entire rational function (see Polynomial). Let  be a unitary module over an associative-commutative ring
be a unitary module over an associative-commutative ring  with a unit. A mapping
with a unit. A mapping 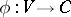 is called a polynomial function if
is called a polynomial function if  , where
, where  is a form of degree
is a form of degree  on
on  ,
, 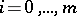 (see Multilinear form). Most frequently, polynomial functions are considered when
(see Multilinear form). Most frequently, polynomial functions are considered when 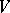 is a free
is a free 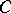 -module (for example, a vector space over a field
-module (for example, a vector space over a field 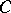 ) having a finite basis
) having a finite basis  . Then the mapping
. Then the mapping 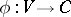 is a polynomial function if and only if
is a polynomial function if and only if  , where
, where 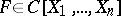 is a polynomial over
is a polynomial over 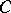 and
and  are the coordinates of an element
are the coordinates of an element 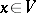 in the basis
in the basis  . If here
. If here 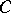 is an infinite integral domain, the polynomial
is an infinite integral domain, the polynomial 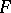 is defined uniquely.
is defined uniquely.
The polynomial functions on a module 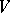 form an associative-commutative
form an associative-commutative 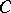 -algebra
-algebra 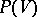 with a unit with respect to the natural operations. If
with a unit with respect to the natural operations. If 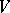 is a free module with a finite basis over an infinite integral domain
is a free module with a finite basis over an infinite integral domain 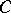 , the algebra
, the algebra 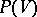 is canonically isomorphic to the symmetric algebra
is canonically isomorphic to the symmetric algebra 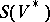 of the adjoint (or dual) module
of the adjoint (or dual) module  , while if
, while if 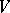 is a finite-dimensional vector space over a field of characteristic 0,
is a finite-dimensional vector space over a field of characteristic 0, 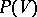 is the algebra of symmetric multilinear forms on
is the algebra of symmetric multilinear forms on 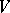 .
.
Comments
E.g., polynomial functions on a Banach space naturally arise when one considers Taylor approximations to a differentiable function on such a space.
Polynomial function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polynomial_function&oldid=16513