Isoperimetric problem
One of the fundamental problems in the classical calculus of variations. The isoperimetric problem consists in minimizing a functional
 |
under constraints of the form
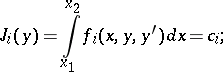 |
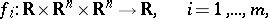 |
and certain boundary conditions.
The isoperimetric problem reduces to the Lagrange problem when new variables  are introduced satisfying the differential equations
are introduced satisfying the differential equations
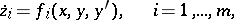 |
with boundary conditions
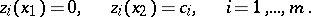 |
Necessary conditions for optimality in the isoperimetric problem have the same form as do the simplest problems in the calculus of variations related to the Lagrange function
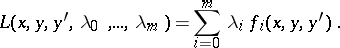 |
The name "isoperimetric problem" goes back to the following classical question: Among all the curves with given perimeter in the plane, find the one that bounds the largest area.
References
| [1] | G.A. Bliss, "Lectures on the calculus of variations" , Chicago Univ. Press (1947) |
| [2] | L.Ya. Tslaf, "Calculus of variations and integral equations" , Moscow (1970) (In Russian) |
| [3] | M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian) |
Comments
As stated above, the original isoperimetric problem is the problem of finding the geometric figure with maximal area and given perimeter. I.e., the problem is to find functions  ,
,  such that
such that
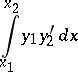 |
is minimized, subject to
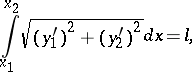 |
where 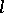 is a given constant.
is a given constant.
References
| [a1] | L.E. [L.E. El'sgol'ts] Elsgolc, "Calculus of variations" , Pergamon (1961) (Translated from Russian) |
Isoperimetric problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isoperimetric_problem&oldid=16510