Decimal fraction

An arithmetical fraction with an integral power of 10 as its denominator. The following notation has been accepted for a decimal fraction:

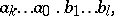(1)

where 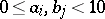are integers and if then is also non-zero.

Formula (1) expresses the number

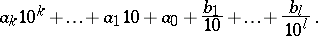For example,

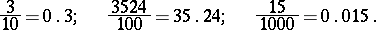The digits to the right of the decimal point are known as the decimal digits. If a decimal fraction contains no integer part, i.e. its absolute value is smaller than one, a zero is placed to the left of the decimal point.

An infinite decimal fraction is an infinite sequence of digits such as

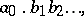(2)

where is an integer, while each one of the numbers , 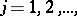assumes one of the values 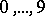. Any real number 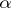is the sum of such a series, i.e.

The partial sums of the series (2) are finite decimal fractions 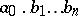, which are approximate values of the number 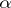smaller than 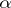; the numbers

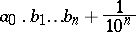are the respective approximate values larger than 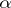. If there exists integers and 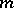such that for all 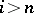the equalities

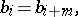are valid, the infinite decimal fraction is said to be periodic. Any finite decimal fraction may be regarded as an infinite periodic fraction with 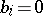for . If 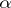is a rational number, the corresponding fraction (2) will be periodic. If 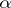is irrational, the fraction (2) cannot be periodic.