Bernstein-von Mises theorem
Let 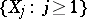 be independent identically distributed random variables with a probability density depending on a parameter
be independent identically distributed random variables with a probability density depending on a parameter 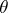 (cf. Random variable; Probability distribution). Suppose that an a priori distribution for
(cf. Random variable; Probability distribution). Suppose that an a priori distribution for 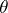 is chosen. One of the fundamental theorems in the asymptotic theory of Bayesian inference (cf. Bayesian approach) is concerned with the convergence of the a posteriori density of
is chosen. One of the fundamental theorems in the asymptotic theory of Bayesian inference (cf. Bayesian approach) is concerned with the convergence of the a posteriori density of 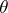 , given
, given 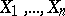 , to the normal density. In other words, the a posteriori distribution tends to look like a normal distribution asymptotically. This phenomenon was first noted in the case of independent and identically distributed observations by P.S. Laplace. A related, but different, result was proved by S.N. Bernstein [a2], who considered the a posteriori distribution of
, to the normal density. In other words, the a posteriori distribution tends to look like a normal distribution asymptotically. This phenomenon was first noted in the case of independent and identically distributed observations by P.S. Laplace. A related, but different, result was proved by S.N. Bernstein [a2], who considered the a posteriori distribution of  given the average
given the average 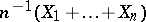 . R. von Mises [a12] extended the result to a posteriori distributions conditioned by a finite number of differentiable functionals of the empirical distribution function. L. Le Cam [a5] studied the problem in his work on asymptotic properties of maximum likelihood and related Bayesian estimates. The Bernstein–von Mises theorem about convergence in the
. R. von Mises [a12] extended the result to a posteriori distributions conditioned by a finite number of differentiable functionals of the empirical distribution function. L. Le Cam [a5] studied the problem in his work on asymptotic properties of maximum likelihood and related Bayesian estimates. The Bernstein–von Mises theorem about convergence in the 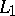 -mean for the case of independent and identically distributed random variables reads as follows, see [a3].
-mean for the case of independent and identically distributed random variables reads as follows, see [a3].
Let 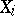 ,
, 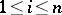 , be independent identically distributed random variables with probability density
, be independent identically distributed random variables with probability density 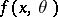 ,
, 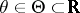 . Suppose
. Suppose  is open and
is open and 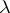 is an a priori probability density on
is an a priori probability density on 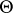 which is continuous and positive in an open neighbourhood of the true parameter
which is continuous and positive in an open neighbourhood of the true parameter 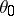 . Let
. Let 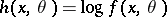 . Suppose that
. Suppose that 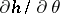 and
and 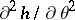 exist and are continuous in
exist and are continuous in 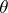 . Further, suppose that
. Further, suppose that 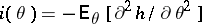 is continuous, with
is continuous, with 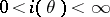 . Let
. Let  be a non-negative function satisfying
be a non-negative function satisfying
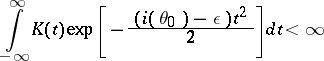 |
for some 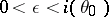 . Let
. Let 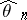 be a maximum-likelihood estimator of
be a maximum-likelihood estimator of 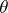 based on
based on 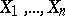 (cf. Maximum-likelihood method) and let
(cf. Maximum-likelihood method) and let 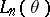 be the corresponding likelihood function. It is known that under certain regularity conditions there exists a compact neighbourhood
be the corresponding likelihood function. It is known that under certain regularity conditions there exists a compact neighbourhood 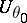 of
of 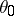 such that:
such that:
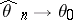 almost surely;
almost surely;
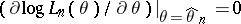 for large
for large  ;
;
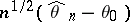 converges in distribution (cf. Convergence in distribution) to the normal distribution with mean
converges in distribution (cf. Convergence in distribution) to the normal distribution with mean  and variance
and variance 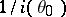 as
as 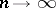 .
.
Let 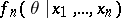 denote the a posteriori density of
denote the a posteriori density of 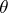 given the observation
given the observation  and the a priori probability density
and the a priori probability density 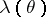 , that is,
, that is,
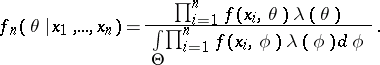 |
Let 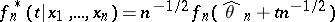 . Then
. Then 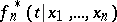 is the a posteriori density of
is the a posteriori density of 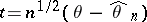 .
.
A generalized version of the Bernstein–von Mises theorem, under the assumptions stated above and some addition technical conditions, is as follows.
If, for every 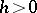 and
and 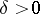 ,
,
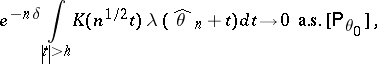 |
then
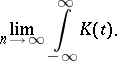 |
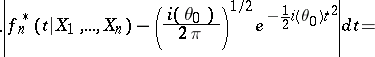 |
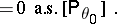 |
For 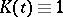 one finds that the a posteriori density converges to the normal density in
one finds that the a posteriori density converges to the normal density in 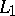 -mean convergence. The result can be extended to a multi-dimensional parameter. As an application of the above theorem, it can be shown that the Bayesian estimator is strongly consistent and asymptotically efficient for a suitable class of loss functions (cf. [a11]). For rates of convergence see [a4], [a7], [a8].
-mean convergence. The result can be extended to a multi-dimensional parameter. As an application of the above theorem, it can be shown that the Bayesian estimator is strongly consistent and asymptotically efficient for a suitable class of loss functions (cf. [a11]). For rates of convergence see [a4], [a7], [a8].
B.L.S. Prakasa Rao [a6] has generalized the result to arbitrary discrete-time stochastic processes (cf. [a1]); for extensions to diffusion processes and diffusion fields, see [a9], [a10].
References
| [a1] | I.V. Basawa, B.L.S. Prakasa Rao, "Statistical inference for stochastic processes" , Acad. Press (1980) |
| [a2] | S.N. Bernstein, "Theory of probability" (1917) (In Russian) |
| [a3] | J.D. Borwanker, G. Kallianpur, B.L.S. Prakasa Rao, "The Bernstein–von Mises theorem for Markov processes" Ann. Math. Stat. , 43 (1971) pp. 1241–1253 |
| [a4] | C. Hipp, R. Michael, "On the Bernstein–von Mises approximation of posterior distribution" Ann. Stat. , 4 (1976) pp. 972–980 |
| [a5] | L. Le Cam, "On some asymptotic properties of maximum likelihood estimates and related Bayes estimates" Univ. California Publ. Stat. , 1 (1953) pp. 277–330 |
| [a6] | B.L.S. Prakasa Rao, "Statistical inference for stochastic processes" G. Sankaranarayanan (ed.) , Proc. Advanced Symp. on Probability and its Applications , Annamalai Univ. (1976) pp. 43–150 |
| [a7] | B.L.S. Prakasa Rao, "Rate of convergence of Bernstein–von Mises approximation for Markov processes" Serdica , 4 (1978) pp. 36–42 |
| [a8] | B.L.S. Prakasa Rao, "The equivalence between (modified) Bayes estimator and maximum likelihood estimator for Markov processes" Ann. Inst. Statist. Math. , 31 (1979) pp. 499–513 |
| [a9] | B.L.S. Prakasa Rao, "The Bernstein–von Mises theorem for a class of diffusion processes" Teor. Sluch. Prots. , 9 (1981) pp. 95–104 (In Russian) |
| [a10] | B.L.S. Prakasa Rao, "On Bayes estimation for diffusion fields" J.K. Ghosh (ed.) J. Roy (ed.) , Statistics: Applications and New Directions , Statistical Publishing Soc. (1984) pp. 504–511 |
| [a11] | B.L.S. Prakasa Rao, "Asymptotic theory of statistical inference" , Wiley (1987) |
| [a12] | R. von Mises, "Wahrscheinlichkeitsrechnung" , Springer (1931) |
Bernstein-von Mises theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein-von_Mises_theorem&oldid=16482