Symmetric matrix
A square matrix in which any two elements symmetrically positioned with respect to the main diagonal are equal to each other, that is, a matrix 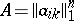 that is equal to its transpose:
that is equal to its transpose:
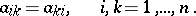 |
A real symmetric matrix of order  has exactly
has exactly  real eigenvalues (counted with multiplicity). If
real eigenvalues (counted with multiplicity). If 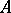 is a symmetric matrix, then so are
is a symmetric matrix, then so are 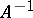 and
and 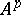 , and if
, and if  and
and 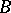 are symmetric matrices of the same order, then
are symmetric matrices of the same order, then 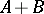 is a symmetric matrix, while
is a symmetric matrix, while 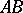 is symmetric if and only if
is symmetric if and only if 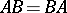 .
.
Comments
Every square complex matrix is similar to a symmetric matrix. A real 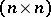 -matrix is symmetric if and only if the associated operator
-matrix is symmetric if and only if the associated operator 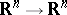 (with respect to the standard basis) is self-adjoint (with respect to the standard inner product). A polar decomposition factors a matrix
(with respect to the standard basis) is self-adjoint (with respect to the standard inner product). A polar decomposition factors a matrix 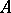 into a product
into a product 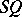 of a symmetric and an orthogonal matrix.
of a symmetric and an orthogonal matrix.
Let 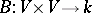 be a bilinear form on a vector space
be a bilinear form on a vector space 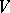 (cf. Bilinear mapping). Then the matrix of
(cf. Bilinear mapping). Then the matrix of 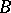 (with respect to the same basis in the two factors
(with respect to the same basis in the two factors 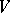 ) is symmetric if and only if
) is symmetric if and only if 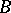 is a symmetric bilinear form, i.e.
is a symmetric bilinear form, i.e.  .
.
References
| [a1] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1959–1960) pp. Vol. 1, Chapt. IX; Vol. 2, Chapt. XI (Translated from Russian) |
| [a2] | W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. Sect. 2.7 |
Symmetric matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_matrix&oldid=16470