Lefschetz formula

A formula that expresses the number of fixed points of an endomorphism of a topological space in terms of the traces of the corresponding endomorphisms in the cohomology groups.

This formula was first established by S. Lefschetz for finite-dimensional orientable topological manifolds [1] and for finite cell complexes (see [2], [3]). These papers of Lefschetz were preceded by a paper of L.E.J. Brouwer (1911) on the fixed point of a continuous mapping of an -dimensional sphere into itself. A new version of the proof of the Lefschetz formula for finite cell complexes was given by H. Hopf (see [9]).

Let 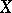be a connected orientable -dimensional compact topological manifold or an -dimensional finite cell complex, let 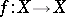be a continuous mapping and let 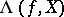be the Lefschetz number of 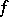. Assume that all fixed points of the mapping 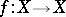are isolated. For each fixed poin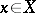t , let 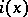be its Kronecker index (the local degree (cf. Degree of a mapping) of 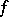in a neighbourhood of ). Then the Lefschetz formula for 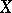and 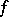has the form

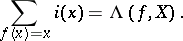(1)

There is, [8], a generalization of the Lefschetz formula to the case of arbitrary continuous mappings of compact Euclidean neighbourhood retracts.

Let 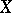be a differentiable compact orientable manifold and let 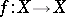be a differentiable mapping. A fixed point 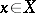for 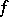is said to be non-singular if it is isolated and if 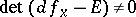, where 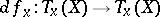is the differential of 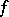at and 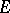is the identity transformation. For a non-singular point 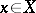its index 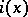coincides with the number 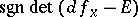. In this case the Lefschetz formula (1) shows that the Lefschetz number 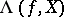is equal to the difference between the number of fixed points with index 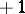and the number of fixed points with index 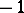; in particular, it does not exceed the total number of fixed points. In this case the left-hand side of (1) can be determined in the same way as the intersection index 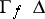on 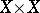, where 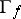is the graph of 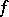and 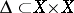is the diagonal (cf. Intersection index (in algebraic geometry)).

A consequence of the Lefschetz formula is the Hopf formula, which asserts that the Euler characteristic 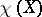is equal to the sum of the indices of the zeros of a global 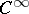-vector field on 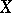(it is assumed that all zeros of are isolated) (see [5]).

There is a version of the Lefschetz formula for compact complex manifolds and the Dolbeault cohomology (see [5]). Let 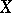be a compact complex manifold of dimension 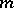and let 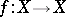a be holomorphic mapping with non-singular fixed points. Let 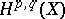be the Dolbeault cohomology of 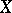of type 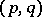(cf. Differential form) and let 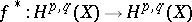be the endomorphism induced by 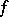. The number

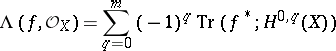is called the holomorphic Lefschetz number. One then has the following holomorphic Lefschetz formula:

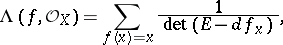where 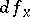is the holomorphic differential of 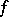at .

In abstract algebraic geometry the Lefschetz formula has served as a starting point in the search for Weil cohomology in connection with Weil's conjectures about zeta-functions of algebraic varieties defined over finite fields (cf. Zeta-function). An analogue of the Lefschetz formula in abstract algebraic geometry has been established for 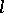-adic cohomology with compact support and with coefficients in constructible 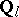-sheaves, where 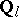is the field of 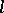-adic numbers and where 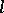is a prime number distinct from the characteristic of the field 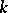. This formula is often called the trace formula.

Let 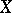be an algebraic variety (or scheme) over a finite field 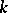, let 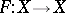be a Frobenius morphism (cf. e.g. Frobenius automorphism), 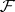a sheaf on 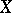, and let 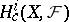be cohomology with compact support of the variety (scheme) 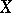with coefficients in 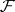. Then the morphism 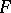determines a cohomology endomorphism

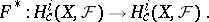If 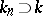is an extension of 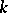of degree and if 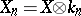, 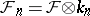are the variety (scheme) and sheaf obtained from 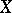and 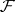by extending the field of scalars, then the corresponding Frobenius morphism 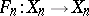coincides with the -th power 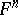of .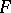

Now let 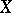be a separable scheme of finite type over the finite field 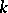of 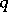elements, let 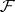be a constructible 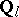-sheaf on , 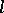a prime number distinct from the characteristic of 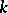, and 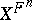the set of fixed geometric points of the morphism 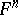or, equivalently, the set 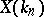of geometric points of the scheme 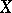with values in the field 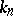. Then for any integer 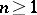the following Lefschetz formula (or trace formula) holds (see [6], [7]):

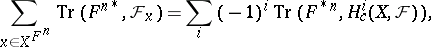(2)

where 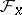is the stalk of 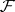over . In the case of the constant sheaf 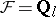one has 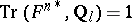and the left-hand side of (2) is none other than the number of geometric points of 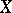with values in 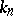. In particular, for 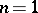this is simply the number of points of 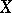with values in the ground field 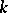. If 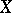is proper over 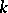(for example, if 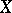is a complete algebraic variety over 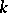), then 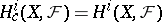and the right-hand side of (2) is an alternating sum of the traces of the Frobenius endomorphism in the ordinary cohomology of .

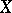There are (see [7]) generalizations of formula (2).

References

[1]	S. Lefschetz, "Intersections and transformations of complexes and manifolds" Trans. Amer. Soc. , 28 (1926) pp. 1–49
[2]	S. Lefschetz, "The residual set of a complex manifold and related questions" Proc. Nat. Acad. Sci. USA , 13 (1927) pp. 614–622
[3]	S. Lefschetz, "On the fixed point formula" Ann. of Math. (2) , 38 (1937) pp. 819–822
[4]	S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386
[5]	P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978)
[6]	P. Deligne, "Cohomologie étale (SGA 4 1/2)" , Lect. notes in math. , 569 , Springer (1977)
[7]	A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie -adique et fonctions . SGA 5" , Lect. notes in math. , 589 , Springer (1977)
[8]	A. Dold, "Lectures on algebraic topology" , Springer (1980)
[9]	H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German)

Comments

For the Lefschetz formula in abstract algebraic geometry and its generalizations by A. Grothendieck see also [a1].

References

[a1]	E. Feitag, R. Kiehl, "Etale cohomology and the Weil conjecture" , Springer (1988)