BCK-algebra
Algebras originally defined by K. Iséki and S. Tanaka in [a7] to generalize the set difference in set theory, and by Y. Imai and Iséki in [a5] as the algebras of certain propositional calculi. A BCK-algebra may be defined as a non-empty set 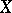 with a binary relation
with a binary relation  and a constant
and a constant  satisfying the following axioms:
satisfying the following axioms:
1) 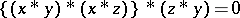 ;
;
2) 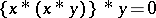 ;
;
3) 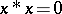 ;
;
4) 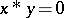 and
and 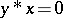 imply
imply 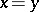 ;
;
5) 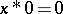 implies
implies 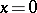 ;
;
6) 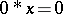 for all
for all  . A partial order
. A partial order 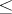 can then be defined by putting
can then be defined by putting 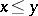 if and only if
if and only if 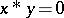 . A very useful property is
. A very useful property is 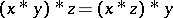 .
.
A BCK-algebra is commutative if it satisfies the identity 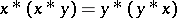 (cf. also Commutative ring). In this case,
(cf. also Commutative ring). In this case, 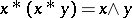 , the greatest lower bound of
, the greatest lower bound of  and
and 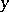 under the partial order
under the partial order 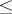 . The BCK-algebra is bounded if it has a largest element. Denoting this element by
. The BCK-algebra is bounded if it has a largest element. Denoting this element by 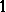 , one has
, one has 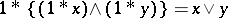 , the least upper bound of
, the least upper bound of  and
and 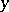 . In this case,
. In this case, 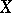 is a distributive lattice with bounds
is a distributive lattice with bounds  and
and 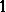 . A BCK-algebra is positive implicative if it satisfies the identity
. A BCK-algebra is positive implicative if it satisfies the identity 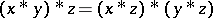 . This is equivalent to the identity
. This is equivalent to the identity 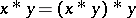 .
.  is called implicative if it satisfies the identity
is called implicative if it satisfies the identity 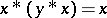 . Every implicative BCK-algebra is commutative and positive implicative, and a bounded implicative BCK-algebra is a Boolean algebra.
. Every implicative BCK-algebra is commutative and positive implicative, and a bounded implicative BCK-algebra is a Boolean algebra.
An ideal of a BCK-algebra is a non-empty set 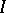 such that
such that 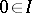 and if
and if 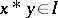 and
and 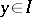 imply
imply 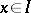 . The ideal is implicative if
. The ideal is implicative if  and
and 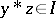 imply
imply 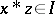 . It is known that always
. It is known that always 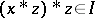 . Note that in a positive implicative BCK-algebra, every ideal is implicative. Implicative ideals are important because in a bounded commutative BCK-algebra they are precisely the ideals for which the quotient BCK-algebras are Boolean algebras. Here, if
. Note that in a positive implicative BCK-algebra, every ideal is implicative. Implicative ideals are important because in a bounded commutative BCK-algebra they are precisely the ideals for which the quotient BCK-algebras are Boolean algebras. Here, if 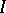 is an ideal in a BCK-algebra, one can define a congruence relation in
is an ideal in a BCK-algebra, one can define a congruence relation in 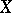 by
by 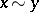 if and only if
if and only if 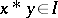 and
and 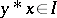 . The set
. The set 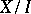 of congruence classes then becomes a BCK-algebra under the operation
of congruence classes then becomes a BCK-algebra under the operation 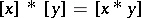 , with
, with 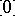 as the constant and
as the constant and 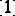 as the largest element if there exists a largest element
as the largest element if there exists a largest element 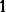 . Some, but not all, of the well-known results on distributive lattices and Boolean algebras hold in BCK-algebras, in particular in bounded commutative BCK-algebras. For example, the prime ideal theorem holds for bounded commutative BCK-algebras, that is, if
. Some, but not all, of the well-known results on distributive lattices and Boolean algebras hold in BCK-algebras, in particular in bounded commutative BCK-algebras. For example, the prime ideal theorem holds for bounded commutative BCK-algebras, that is, if 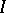 is an ideal and
is an ideal and 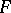 is a lattice filter such that
is a lattice filter such that 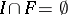 , then there exists a prime ideal
, then there exists a prime ideal 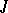 such that
such that 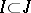 and
and  . Here, "prime ideal" simply means that if it contains
. Here, "prime ideal" simply means that if it contains 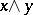 , then it contains either
, then it contains either  or
or 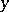 .
.
Some of the homological algebra properties of BCK-algebras are known, see [a2]. There is also a close connection between BCK-algebras and commutative 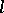 -groups with order units (cf.
-groups with order units (cf. 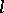 -group). Recall that an element
-group). Recall that an element  in the positive cone
in the positive cone 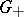 of a commutative
of a commutative 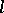 -group
-group 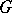 is an order unit if for each
is an order unit if for each 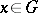 one has
one has 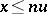 for some integer
for some integer  . Let
. Let 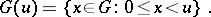 For
For 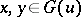 , let
, let 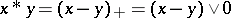 . Then
. Then 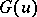 is a commutative BCK-algebra.
is a commutative BCK-algebra.
Fuzzy ideals of BCK-algebras are described in [a3] and [a4]. General references for BCK-algebras are [a6] and [a7].
References
| [a1] | C.S. Hoo, P.V. Ramana Murty, "The ideals of a bounded commutative BCK-algebra" Math. Japon. , 32 (1987) pp. 723–733 |
| [a2] | C.S. Hoo, "Injectives in the categories of BCK and BCI-algebras" Math. Japon. , 33 (1988) pp. 237–246 |
| [a3] | C.S. Hoo, "Fuzzy ideals of BCI and MV-algebras" Fuzzy Sets and Systems , 62 (1994) pp. 111–114 |
| [a4] | C.S. Hoo, "Fuzzy implicative and Boolean ideals of MV-algebras" Fuzzy Sets and Systems , 66 (1994) pp. 315–327 |
| [a5] | Y. Imai, K. Iséki, "On axiom systems of propositional calculi, XIV" Proc. Japan Acad. Ser. A, Math. Sci. , 42 (1966) pp. 19–22 |
| [a6] | K. Iséki, S. Tanaka, "Ideal theory of BCK-algebras" Math. Japon. , 21 (1976) pp. 351–366 |
| [a7] | K. Iséki, S. Tanaka, "An introduction to the theory of BCK-algebras" Math. Japon. , 23 (1978) pp. 1–26 |
BCK-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=BCK-algebra&oldid=16457