Limit
One of the fundamental concepts in mathematics, meaning that a variable depending on another variable arbitrary closely approaches some constant as the latter variable changes in a definite manner. In the definition of a limit, the concept of nearness of the objects under consideration plays a fundamental role: only after a definition of nearness does a limit acquire an exact meaning. The following fundamental concepts of mathematical analysis are connected with that of a limit: continuity, derivative, differential, integral. One of the simplest cases of a limit is the limit of a sequence.
The limit of a sequence.
Let 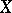 be a topological space. A sequence of points
be a topological space. A sequence of points 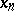 ,
, 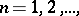 of
of 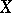 is said to converge to a point
is said to converge to a point 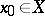 or, which is the same, the point
or, which is the same, the point 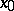 is said to be a limit of the given sequence if for each neighbourhood
is said to be a limit of the given sequence if for each neighbourhood 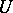 of
of 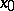 there is a natural number
there is a natural number 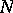 such that for all
such that for all 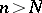 the membership
the membership 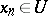 is satisfied. In this case one writes
is satisfied. In this case one writes
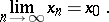 |
In the case when 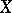 is a Hausdorff space, the limit of a sequence
is a Hausdorff space, the limit of a sequence 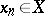 ,
, 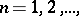 is unique, provided that it exists. For a metric space
is unique, provided that it exists. For a metric space 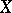 , a point
, a point 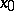 is the limit of a sequence
is the limit of a sequence 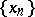 if and only if for each
if and only if for each 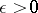 there is a natural number
there is a natural number 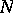 such that for all indices
such that for all indices 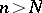 the inequality
the inequality 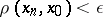 is satisfied, where
is satisfied, where 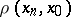 is the distance between
is the distance between 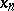 and
and 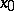 . If a sequence of points of a metric space is convergent, then it is bounded. A sequence of points of a complete metric space is convergent if and only if it is a fundamental sequence. In particular, this is true for sequences of numbers, for which the concept of a limit of a sequence historically arose first. For such sequences the following formulas hold:
. If a sequence of points of a metric space is convergent, then it is bounded. A sequence of points of a complete metric space is convergent if and only if it is a fundamental sequence. In particular, this is true for sequences of numbers, for which the concept of a limit of a sequence historically arose first. For such sequences the following formulas hold:
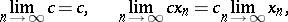 |
where  is any given number;
is any given number;
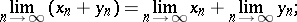 |
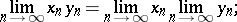 |
and if 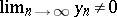 , then
, then
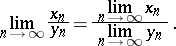 |
These properties of sequences of numbers can be carried over to limits of sequences in more general structures, for example, the property of the limit of a sum — to sequences of points in linear topological spaces, the property of the limit of a product — to sequences of points in a topological group, etc.
If two real sequences 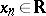 and
and 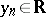 are convergent and if
are convergent and if 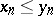 ,
, 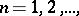 then
then
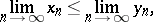 |
i.e. non-strict inequalities are preserved under limit transition. If
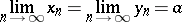 |
and if 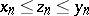 , then the sequence
, then the sequence 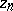 ,
, 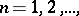 converges to the same limit:
converges to the same limit: 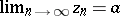 . These properties can be generalized to limits of sequences of points in ordered sets.
. These properties can be generalized to limits of sequences of points in ordered sets.
Every increasing (decreasing) sequence of real numbers 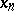 , i.e. such that
, i.e. such that 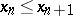 (
(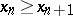 ),
), 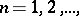 that is bounded from above (below) is convergent and its limit is the supremum (infimum) of the set of its members. For example, if
that is bounded from above (below) is convergent and its limit is the supremum (infimum) of the set of its members. For example, if 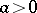 ,
, 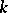 is a natural number and
is a natural number and 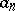 is an approximate value of the root
is an approximate value of the root 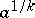 calculated up to
calculated up to  decimal places after the decimal point, then the
decimal places after the decimal point, then the 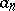 ,
, 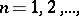 form an increasing sequence and
form an increasing sequence and 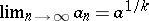 . Another example of an increasing sequence which is bounded from above is the sequence of perimeters of regular polygons with
. Another example of an increasing sequence which is bounded from above is the sequence of perimeters of regular polygons with  sides,
sides, 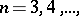 inscribed in some circle; this sequence converges to the length of the circle.
inscribed in some circle; this sequence converges to the length of the circle.
In the theory of sequences of numbers a fundamental role is played by infinitesimal sequences or null sequences, i.e. those sequences which converge to zero. The general concept of a sequence of numbers can be reduced to that of an infinitesimal sequence in the sense that a sequence of numbers converges to a given number if and only if the differences between the terms of the sequence and the given number form an infinitesimal sequence.
The concept of an infinitely-large sequence of numbers is also useful. These are the sequences with as limits one of the infinities 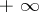 ,
, 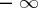 , or the infinity
, or the infinity  without a sign. For the definition of infinite limits, the concept of
without a sign. For the definition of infinite limits, the concept of  -neighbourhoods,
-neighbourhoods, 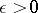 , of the symbols
, of the symbols 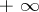 ,
, 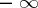 or
or 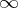 in the set
in the set 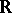 of real numbers is introduced by the formulas
of real numbers is introduced by the formulas
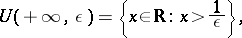 |
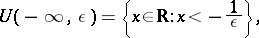 |
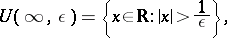 |
and the concept of the  -neighbourhood of
-neighbourhood of 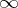 in the set
in the set 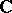 of complex numbers is introduced by the formula
of complex numbers is introduced by the formula
 |
One writes 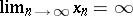 (
(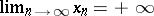 or
or 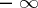 ),
), 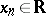 ,
, 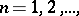 if for each
if for each 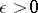 there is an index
there is an index 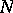 such that for all indices
such that for all indices 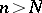 the membership
the membership 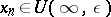 (
(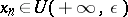 or
or 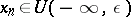 ) is satisfied. The infinite limit of a sequence of complex numbers is defined similarly.
) is satisfied. The infinite limit of a sequence of complex numbers is defined similarly.
Every bounded sequence of numbers contains a convergent subsequence (cf. Bolzano–Weierstrass theorem). Every unbounded sequence contains an infinitely-large sequence.
A (finite or infinite) limit of a subsequence of a given sequence is called a subsequential limit of the latter. In the set of subsequential limits of any sequence of real numbers there is always a largest one and a smallest one (finite or infinite). The largest (smallest) subsequential limit of a sequence is called its upper (lower) limit. A sequence has a finite or infinite limit if and only if its upper limit coincides with its lower limit, and then their common value is the limit of the sequence.
Other concepts of a limit, for example, the limit of a function and of Riemann sums, can be expressed in terms of the limit of a sequence. The definition of the limit of a sequence can be generalized to directed (partially ordered) sets.
The limit of a function (mapping).
Let 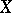 and
and 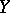 be topological spaces,
be topological spaces, 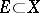 ,
, 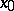 an accumulation point (or a cluster point) of
an accumulation point (or a cluster point) of 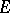 , and let
, and let 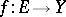 be a mapping from
be a mapping from 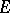 into
into 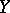 . A point
. A point 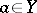 is called a limit of the mapping
is called a limit of the mapping 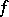 at
at 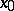 (or, as one says, as
(or, as one says, as  approaches
approaches 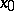 ), in symbols,
), in symbols,
 |
if for any neighbourhood 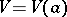 of
of  in
in 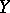 there is a neighbourhood
there is a neighbourhood 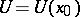 of
of 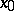 in
in 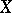 , such that for any point
, such that for any point 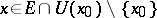 the image
the image 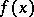 belongs to
belongs to 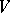 :
: 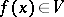 . In other words, if
. In other words, if 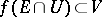 . If
. If 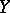 is a Hausdorff space, then the mapping
is a Hausdorff space, then the mapping 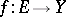 can have only one limit at a given point
can have only one limit at a given point 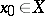 .
.
In the case where 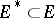 and
and 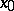 is an accumulation point of
is an accumulation point of 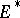 , a limit of the restriction
, a limit of the restriction 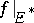 of
of 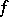 to
to 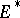 is called a limit of
is called a limit of 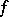 on
on 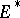 , in symbols,
, in symbols,
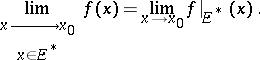 |
If 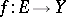 ,
, 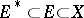 ,
, 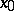 is an accumulation point of
is an accumulation point of 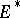 , and
, and 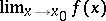 exists, then the limit of
exists, then the limit of 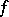 at
at 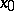 also exists on
also exists on 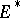 and
and
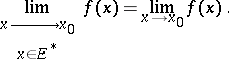 |
If 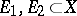 ,
, 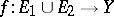 and the limits
and the limits
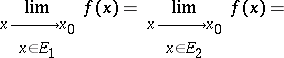 |
exist, then the limit
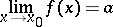 |
also exists.
In considering the limit of a mapping (function) 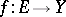 ,
, 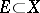 , as
, as 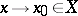 , it may happen that
, it may happen that 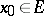 or, on the other hand,
or, on the other hand, 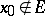 . The case
. The case 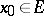 is of special interest, because it leads to the concept of a continuous function: If
is of special interest, because it leads to the concept of a continuous function: If 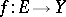 ,
, 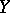 is a Hausdorff space and
is a Hausdorff space and 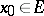 , then for the mapping
, then for the mapping 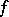 to be continuous at
to be continuous at 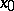 it is necessary and sufficient that
it is necessary and sufficient that
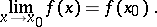 |
If 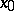 is an isolated point of
is an isolated point of 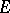 , then the limit
, then the limit
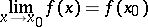 |
always exists, for any mapping 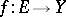 , i.e. any mapping
, i.e. any mapping 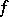 is continuous at all isolated points of its domain. Therefore, the concept of a limit of a mapping, in particular, of continuity, is non-trivial only for limit points of the set being mapped (cf. Limit point of a set). In the classical case of the limit of a function
is continuous at all isolated points of its domain. Therefore, the concept of a limit of a mapping, in particular, of continuity, is non-trivial only for limit points of the set being mapped (cf. Limit point of a set). In the classical case of the limit of a function 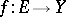 it is usually assumed that
it is usually assumed that 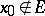 , i.e.
, i.e. 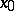 does not belong to the set on which the limit is taken.
does not belong to the set on which the limit is taken.
If the space 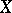 satisfies the first axiom of countability at the point
satisfies the first axiom of countability at the point 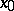 and the space
and the space 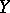 is Hausdorff, then for the existence of the limit
is Hausdorff, then for the existence of the limit 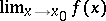 of a mapping
of a mapping 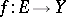 ,
, 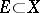 , it is necessary and sufficient that for any sequence
, it is necessary and sufficient that for any sequence 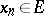 ,
, 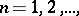 such that
such that 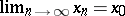 , the limit
, the limit 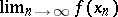 exists. If this condition holds, the limit
exists. If this condition holds, the limit 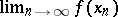 does not depend on the choice of the sequence
does not depend on the choice of the sequence 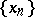 , and the common value of these limits is the limit of
, and the common value of these limits is the limit of 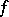 at
at 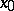 .
.
The limit of a sequence of points 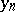 in a topological space
in a topological space 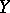 is a special case of the limit of a mapping (function): in this case
is a special case of the limit of a mapping (function): in this case 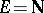 , the set of natural numbers with the discrete topology,
, the set of natural numbers with the discrete topology, 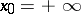 ,
, 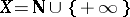 , and a neighbourhood of
, and a neighbourhood of 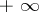 in
in 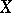 is any subset
is any subset 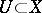 of the form
of the form 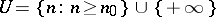 , where
, where 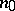 is a natural number.
is a natural number.
The concept of the limit of a multiple sequence, i.e. of a sequence the members of which are indexed by integral multi-indices, is also a special case of the limit of a mapping.
An intrinsic criterion for the existence of the limit of a mapping 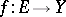 at a given point
at a given point 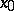 (called the Cauchy criterion) in the case where the space
(called the Cauchy criterion) in the case where the space 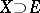 is first countable at
is first countable at 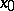 and
and 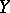 is a complete metric space, is that the limit
is a complete metric space, is that the limit 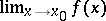 exists if and only if for each
exists if and only if for each 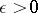 there is a neighbourhood
there is a neighbourhood 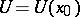 of
of 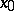 in
in 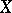 such that for all points
such that for all points 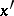 and
and 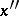 satisfying the condition
satisfying the condition 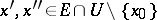 , the inequality
, the inequality 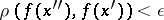 holds. In particular, this criterion is valid if
holds. In particular, this criterion is valid if 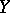 is the set of real or complex numbers.
is the set of real or complex numbers.
Some properties of the limit.
If 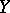 is a metric space,
is a metric space, 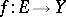 ,
, 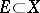 , and the limit
, and the limit 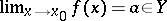 exists, then there is a neighbourhood
exists, then there is a neighbourhood 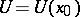 of
of 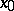 such that the image of the intersection
such that the image of the intersection 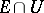 of the set
of the set 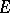 being mapped and the neighbourhood
being mapped and the neighbourhood 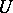 under the mapping
under the mapping 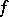 is a bounded subset of
is a bounded subset of 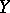 .
.
If a function 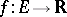 ,
, 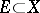 , where
, where 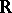 is the set of real numbers, has a finite non-zero limit at a point
is the set of real numbers, has a finite non-zero limit at a point 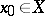 , then there exist a neighbourhood
, then there exist a neighbourhood 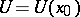 of
of 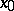 and a number
and a number 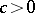 such that for all points
such that for all points 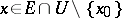 the inequalities
the inequalities
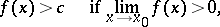 |
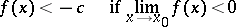 |
are satisfied.
If 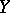 is a topological group (in particular, an Abelian group with group operation written additively),
is a topological group (in particular, an Abelian group with group operation written additively), 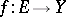 ,
, 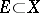 , and
, and 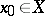 , then the limit
, then the limit 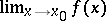 exists and equals
exists and equals  if and only if the function
if and only if the function 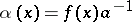 has a limit at
has a limit at 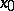 which is equal to the identity element of
which is equal to the identity element of 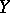 (respectively, the function
(respectively, the function 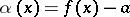 has a limit at
has a limit at 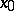 which is equal to zero — such functions are called infinitesimal functions).
which is equal to zero — such functions are called infinitesimal functions).
If 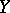 is a linear topological space over a field
is a linear topological space over a field 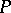 ,
, 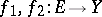 , and
, and 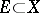 , then the limit of a linear combination of
, then the limit of a linear combination of 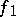 and
and 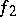 at
at 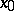 is equal to the same linear combination of their limits at the same point:
is equal to the same linear combination of their limits at the same point:
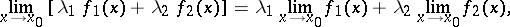 |
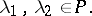 |
If 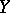 is the set of real or complex numbers,
is the set of real or complex numbers, 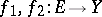 (such functions are called numerical) and
(such functions are called numerical) and 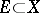 , then
, then
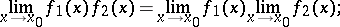 |
if 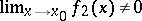 , then
, then
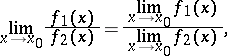 |
and in this case, by the limit 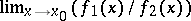 is meant the limit of the restriction of
is meant the limit of the restriction of 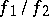 to the intersection of the set
to the intersection of the set 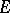 being mapped and some neighbourhood of
being mapped and some neighbourhood of 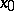 , such that on this intersection the quotient
, such that on this intersection the quotient 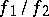 is defined. If
is defined. If 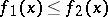 ,
, 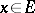 , and the limits
, and the limits 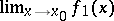 and
and 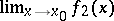 exist, then
exist, then
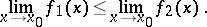 |
If 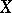 and
and 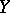 are obtained from the set
are obtained from the set 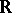 of real numbers by completing it either with an infinity without a sign
of real numbers by completing it either with an infinity without a sign 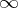 or by two signed infinities
or by two signed infinities 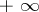 and
and 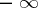 , and
, and 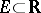 ,
, 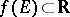 , and
, and 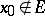 , then the definition of the limit of a function as defined above is the classical definition of a finite or infinite limit of a real-valued function of one real variable. Similarly, if the spaces
, then the definition of the limit of a function as defined above is the classical definition of a finite or infinite limit of a real-valued function of one real variable. Similarly, if the spaces 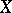 and
and 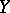 are obtained by completing the set
are obtained by completing the set 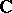 of complex numbers by the infinity
of complex numbers by the infinity 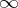 , then the definition of a (finite or infinite) limit of a function of a complex variable is obtained. On the other hand, if the space
, then the definition of a (finite or infinite) limit of a function of a complex variable is obtained. On the other hand, if the space 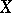 is obtained by completing
is obtained by completing 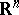 (
(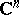 ),
), 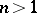 , by the infinity
, by the infinity 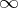 , then the definition of a finite or infinite limit of a function of several variables as the argument approaches a finite point or infinity is obtained.
, then the definition of a finite or infinite limit of a function of several variables as the argument approaches a finite point or infinity is obtained.
For functions defined on subsets of the real line (or, more generally, on ordered sets), the concept of a one-sided limit is defined. Examples of functions having at least one one-sided limit at all limit points of their domain are the real-valued monotone functions: If a function 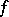 is monotone (cf. Monotone function) on a set
is monotone (cf. Monotone function) on a set 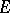 of the real line and the point
of the real line and the point 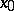 is a limit point of
is a limit point of 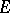 , then it is a limit point of at least one of the sets
, then it is a limit point of at least one of the sets 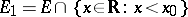 or
or 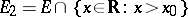 . If
. If 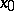 is a limit point of
is a limit point of 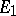 , then
, then 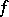 has a limit from the left at
has a limit from the left at 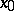 , i.e. on
, i.e. on 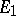 . On the other hand, if
. On the other hand, if 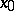 is a limit point of
is a limit point of 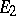 , then
, then 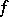 has a limit from the right at
has a limit from the right at 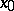 i.e. on
i.e. on 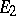 . If, in addition, for example,
. If, in addition, for example, 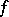 is increasing and bounded from above,
is increasing and bounded from above, 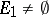 and
and 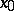 is a limit point of
is a limit point of 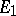 , then the limit
, then the limit 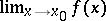 is finite.
is finite.
A fundamental general method for finding the limit of a function is the determination of the principal parts of the function in a neighbourhood of the given point, which is often done by means of the Taylor formula. For the calculation of a limit, the l'Hospital rule is often useful.
In spite of the great generality of the concept of a limit of a mapping, it does not include all existing concepts of a limit appearing in contemporary mathematics. For example, the concept of the limit of Riemann sums (cf. Integral sum) is not included in the concept of the limit of a mapping (function). A sufficiently general concept of a limit, including all fundamental cases in a certain sense, is the concept of the limit of a mapping with respect to a filter.
The limit of a filter.
Let 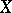 be a topological space,
be a topological space, 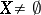 , let
, let 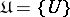 be a base for its topology, and let
be a base for its topology, and let 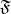 be a filter on
be a filter on 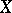 (i.e. a non-empty family
(i.e. a non-empty family 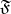 of non-empty subsets of
of non-empty subsets of 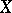 such that for any
such that for any 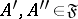 there is an
there is an 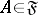 such that
such that 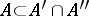 and such that every subset of
and such that every subset of 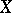 containing an
containing an  belongs to
belongs to 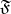 ). A point
). A point 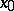 is called a limit of the filter
is called a limit of the filter 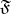 , or its limit point, if
, or its limit point, if 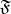 is stronger than the filter
is stronger than the filter 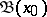 consisting of a local base for the topology at
consisting of a local base for the topology at 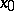 , i.e. for any
, i.e. for any 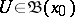 there is an
there is an 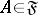 such that
such that 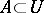 .
.
Let 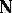 be the set of natural numbers with the discrete topology. The filter on
be the set of natural numbers with the discrete topology. The filter on 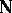 consisting of the complements of all finite subsets of
consisting of the complements of all finite subsets of 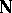 is called the natural filter on
is called the natural filter on 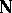 and is denoted by
and is denoted by 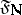 . It does not have a limit in
. It does not have a limit in 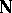 . The same filter on the set
. The same filter on the set 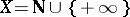 , in which the local base
, in which the local base 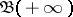 consists of the sets
consists of the sets 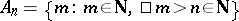 and
and 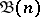 consists of the singleton
consists of the singleton 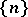 for
for 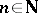 , has
, has 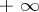 as its limit. Uniqueness of the limit of a filter on a topological space is connected with being able to separate points of the space; in order that every filter on a topological space has at most one limit it is necessary and sufficient that the space be a Hausdorff space.
as its limit. Uniqueness of the limit of a filter on a topological space is connected with being able to separate points of the space; in order that every filter on a topological space has at most one limit it is necessary and sufficient that the space be a Hausdorff space.
Let 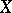 be a set,
be a set, 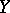 a topological space,
a topological space, 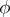 a mapping from
a mapping from 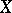 into
into 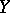 , and
, and 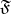 a filter on
a filter on 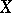 . A point
. A point 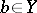 is called the limit of the mapping
is called the limit of the mapping 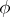 with respect to the filter
with respect to the filter 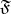 , in symbols,
, in symbols,
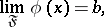 |
if the filter 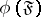 consisting of all sets
consisting of all sets 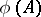 ,
, 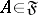 , has
, has 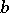 as its limit in
as its limit in 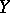 .
.
If 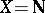 is the set of natural numbers,
is the set of natural numbers, 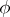 is a mapping from
is a mapping from 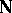 into a topological space
into a topological space 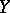 ,
, 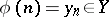 ,
, 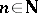 , and
, and 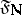 is the natural filter, then the limit of
is the natural filter, then the limit of 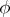 with respect to
with respect to 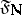 in
in 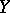 coincides with the usual limit of the sequence
coincides with the usual limit of the sequence 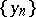 in
in 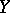 .
.
If in 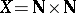 , the filter
, the filter 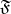 on
on 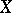 is the product of two natural filters
is the product of two natural filters 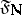 , i.e. it consists of all sets of the form
, i.e. it consists of all sets of the form 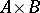 , where
, where 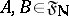 , and if
, and if 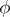 is a mapping from
is a mapping from 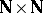 into a topological space
into a topological space 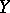 ,
, 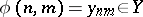 ,
, 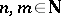 , then the limit of
, then the limit of 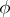 with respect to
with respect to 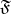 in
in 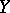 coincides with the usual limit of the double sequence
coincides with the usual limit of the double sequence 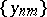 in
in 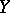 .
.
Let the elements of a set 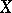 , in turn, be the sets
, in turn, be the sets  consisting of a partition
consisting of a partition 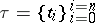 of some interval
of some interval 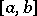 ,
, 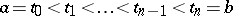 , and points
, and points 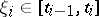 ,
, 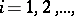 i.e.
i.e.
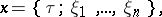 |
Let 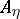 (for any
(for any 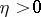 ) be the subset of
) be the subset of 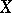 consisting of all elements
consisting of all elements 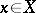 for which the mesh of the partition
for which the mesh of the partition 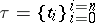 appearing in
appearing in  is smaller than
is smaller than 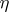 , i.e.
, i.e.
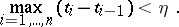 |
The system 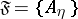 is a filter. Every real-valued function
is a filter. Every real-valued function 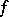 defined on
defined on 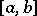 induces a mapping
induces a mapping 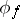 of
of 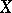 into
into 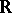 by the formula
by the formula
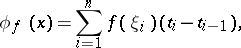 |
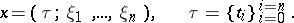 |
Therefore, 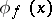 is the Riemann sum of
is the Riemann sum of 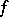 corresponding to
corresponding to 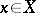 .
.
The limit of 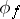 in
in 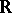 with respect to
with respect to 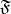 coincides with the usual limit of the Riemann sums of
coincides with the usual limit of the Riemann sums of 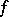 as the mesh of the partition converges to zero. This coincidence holds in the sense that both limits simultaneously exist or not, and if they do so, then they are equal and coincide with the Riemann integral of
as the mesh of the partition converges to zero. This coincidence holds in the sense that both limits simultaneously exist or not, and if they do so, then they are equal and coincide with the Riemann integral of 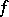 over
over 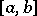 .
.
The limit of a mapping of topological spaces with respect to a filter.
Let 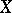 and
and 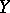 be topological spaces,
be topological spaces, 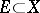 , let
, let 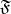 be a filter on
be a filter on 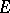 , and let
, and let 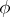 be a mapping from
be a mapping from 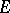 into
into 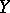 . A point
. A point 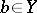 is called the limit of the mapping
is called the limit of the mapping 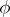 at
at 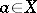 with respect to the filter
with respect to the filter 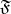 if
if  is the limit of
is the limit of 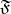 and
and 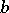 is the limit of
is the limit of 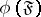 ; notation:
; notation:
 |
If 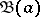 is a neighbourhood base at
is a neighbourhood base at  ,
, 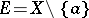 and the filter consists of all "punctured" neighbourhoods
and the filter consists of all "punctured" neighbourhoods 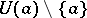 of
of  ,
, 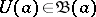 , then the limit
, then the limit 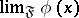 coincides with the usual limit
coincides with the usual limit 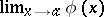 of
of 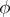 at
at  , i.e. it generalizes the classical definition of the limit of a mapping as formulated in terms of neighbourhoods. An immediate generalization of the concept of the limit of a sequence is the limit of a directed set in a topological space, i.e. a partially ordered set in which any two elements have a common successor. The concept of a limit of a mapping from one topological space into another can be formulated in terms of limits with respect to directed sets (cf. Generalized sequence; Convergence, types of).
, i.e. it generalizes the classical definition of the limit of a mapping as formulated in terms of neighbourhoods. An immediate generalization of the concept of the limit of a sequence is the limit of a directed set in a topological space, i.e. a partially ordered set in which any two elements have a common successor. The concept of a limit of a mapping from one topological space into another can be formulated in terms of limits with respect to directed sets (cf. Generalized sequence; Convergence, types of).
The limit of a sequence of sets.
The topological limit. Let 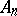 ,
, 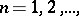 be subsets of a topological space
be subsets of a topological space 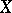 . The upper topological limit
. The upper topological limit 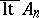 of the sequence
of the sequence  is, by definition, the set of those points
is, by definition, the set of those points 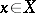 every neighbourhood of which intersects infinitely many sets
every neighbourhood of which intersects infinitely many sets 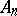 . The lower topological limit
. The lower topological limit 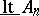 is the set of those points every neighbourhood of which contains points of almost-all sets
is the set of those points every neighbourhood of which contains points of almost-all sets 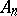 . It is obvious that
. It is obvious that 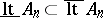 . If
. If 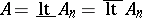 , then the sequence
, then the sequence 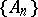 is called convergent and the set
is called convergent and the set 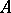 its topological limit; one writes
its topological limit; one writes 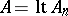 . The upper and lower topological limits of a sequence are closed sets.
. The upper and lower topological limits of a sequence are closed sets.
The set-theoretical limit. There is a concept of the limit of a sequence of sets not involving topology. A sequence 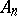 ,
, 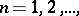 of sets is called convergent if there is a set
of sets is called convergent if there is a set 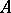 , called its limit and denoted by
, called its limit and denoted by
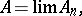 |
such that every element of 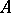 belongs to all sets
belongs to all sets 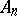 from some index onwards and such that every point of the union of all
from some index onwards and such that every point of the union of all 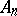 not belonging to
not belonging to 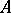 is contained in only finitely many sets
is contained in only finitely many sets 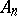 . The set
. The set 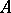 is the limit of the sequence
is the limit of the sequence 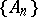 if and only if the upper and lower limits of the sequence coincide and are equal to
if and only if the upper and lower limits of the sequence coincide and are equal to 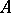 .
.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | V.A. Il'in, V.A. Sadovnichii, B.Kh. Sendov, "Mathematical analysis" , Moscow (1979) (In Russian) |
| [3] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1–3 , Moscow (1988–1989) (In Russian) |
| [4] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [5] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [6] | M. Zamansky, "Introduction à l'algèbre et l'analyse modernes" , Dunod (1958) |
| [7] | A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
| [8] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
Comments
For the general theory of topological spaces one needs to study more general convergence concepts than that of sequences of points. One needs to consider limits of sets of points indexed by a directed partially ordered set (cf. Directed set). Such sets are called nets, and the convergence of nets is sometimes known as Moore–Smith convergence.
The basic (inductive) idea of "limit" is that of some object being approximated arbitrarily closely by a sequence of other objects. There are also various algebraic and categorical implementations of this idea.
Let 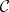 be a category and
be a category and 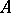 a partially ordered set. A diagram
a partially ordered set. A diagram 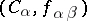 in
in 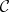 indexed by
indexed by 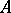 consists of an object
consists of an object 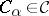 for each
for each 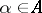 and a morphism
and a morphism 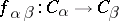 for each
for each 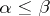 in
in 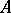 , such that
, such that 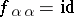 ,
, 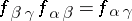 if
if 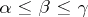 .
.
The projective limit (or inverse limit) 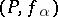 of
of 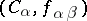 consists of an object
consists of an object 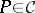 together with morphisms
together with morphisms 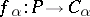 such that
such that 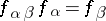 if
if 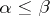 and such that if, moreover,
and such that if, moreover, 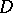 and
and 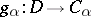 are such that
are such that 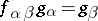 for all
for all 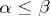 , then there is a unique morphism
, then there is a unique morphism 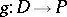 such that
such that 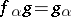 . Notation:
. Notation: 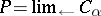 .
.
Dually, the inductive limit (or directed limit) 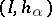 of
of 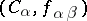 consists of an object
consists of an object 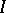 together with morphisms
together with morphisms 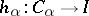 such that
such that 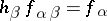 for all
for all 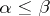 and such that if, moreover,
and such that if, moreover, 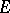 and
and 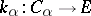 are such that
are such that 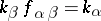 for all
for all 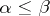 , then there is a unique morphism
, then there is a unique morphism  such that
such that 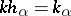 . Notation:
. Notation: 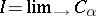 .
.
These are very general notions and include direct products and direct sums (when every pair of points in 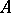 is incomparable). In case
is incomparable). In case 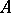 is directed (cf. Directed set), the idea of better and better approximations again reemerges; cf. e.g. Topological vector space.
is directed (cf. Directed set), the idea of better and better approximations again reemerges; cf. e.g. Topological vector space.
More generally one also considers projective and inductive limits of diagrams in categories (cf. Diagram).
Still another limit concept is that of the limit of a spectral sequence: If the spectral sequence 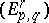 converges to, say,
converges to, say, 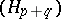 , then
, then 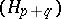 is also called the limit of
is also called the limit of 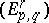 .
.
Still other limit ideas are embodied, for example, by the concepts limit cycle; limit elements (cf. the supplementary material section of Vol. 10); limit point of a set; accumulation point; cluster point; etc.
References
| [a1] | R. Courant, "Differential and integral calculus" , 1–2 , Blackie (1948) (Translated from German) |
| [a2] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
| [a3] | J.L. Kelley, "General topology" , v. Nostrand (1955) pp. 125; 127 |
| [a4] | B. Mitchell, "Theory of categories" , Acad. Press (1965) pp. 7 |
| [a5] | J. Adámek, "Theory of mathematical structures" , Reidel (1983) |
Limit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit&oldid=16444