Algebra with associative powers

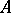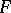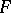A linear algebra over a field each element of which generates an associative subalgebra. The set of all algebras with associative powers over a given field forms a variety of algebras which, if the characteristic of the field is zero, is defined by the system of identities

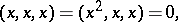where 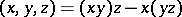. If 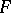is an infinite field of prime characteristic 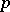, then the variety of algebras with associative powers cannot be defined by any finite system of identities, but an independent, infinite system of identities which defines it is known [3]. If a commutative algebra 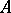with associative powers of characteristic other than 2 has an idempotent 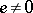, then 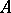can be decomposed according to Peirce into a direct sum of vector subspaces:

(*)

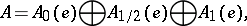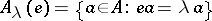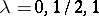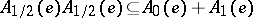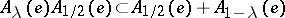where , . Here and are subalgebras, , , for 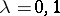. The decomposition (*) plays a fundamental role in the structure theory of algebras with associative powers.

References

[1]	A.A. Albert, "Power-associative rings" Trans. Amer. Math. Soc. , 64 (1948) pp. 552–593
[2]	A.T. Gainov, "Identity relations for binary Lie rings" Uspekhi Mat. Nauk , 12 : 3 (1957) pp. 141–146 (In Russian)
[3]	A.T. Gainov, "Power-associative algebras over a finite-characteristic field" Algebra and Logic , 9 : 1 (1970) pp. 5–19 Algebra i Logika , 9 : 1 (1970) pp. 9–33

Comments

An algebra with associative powers is also called a power-associative algebra. The fact that the set of algebras with associative powers over a field of non-zero characteristic forms a variety defined by 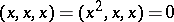was proved in [a1].

References

[a1]	A.A. Albert, "On the power associativity of rings" Summa Brasiliensis Math. , 2 (1948) pp. 21–33