Relative topology
From Encyclopedia of Mathematics
of a subset 
of a topological space 
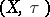
The system of intersections of all possible open subsets of 
(i.e. of elements of the topology 
) with 
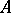. The relative topology is often called the induced topology.
A subset of the topological space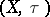 
equipped with the relative topology is called a subspace of 
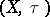. A subspace of a 
-space is itself a 
-space,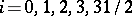 
(cf. Separation axiom). A subspace of a metrizable space is itself metrizable. Any Tikhonov space of weight 
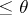is homeomorphic to a subspace of a Hausdorff compactum of weight 
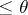(Tikhonov's theorem).
Comments
References
| [a1] | J.L. Kelley, "General topology" , v. Nostrand (1955) pp. 50ff |
How to Cite This Entry:
Relative topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Relative_topology&oldid=16381
Relative topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Relative_topology&oldid=16381
This article was adapted from an original article by B.A. Pasynkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article