Archimedean spiral
A plane transcendental curve the equation of which in polar coordinates has the form:
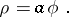 |
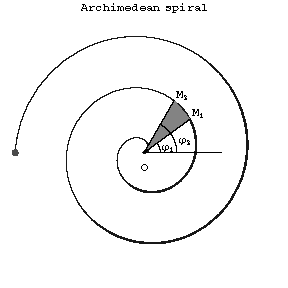
Figure: a013150a
It is described by a point 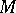 moving at a constant rate along a straight line
moving at a constant rate along a straight line 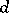 that rotates around a point
that rotates around a point 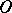 lying on that straight line. At the starting point of the motion,
lying on that straight line. At the starting point of the motion, 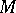 coincides with the centre of rotation
coincides with the centre of rotation 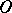 of the straight line (see Fig.). The length of the arc between the points
of the straight line (see Fig.). The length of the arc between the points 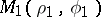 and
and 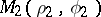 is
is
 |
The area of the sector bounded by an arc of the Archimedean spiral and two radius vectors 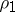 and
and 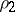 , corresponding to angles
, corresponding to angles 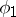 and
and  , is
, is
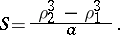 |
An Archimedean spiral is a so-called algebraic spiral (cf. Spirals). The generalization of the Archimedean spiral is called a neoid, the equation of which in polar coordinates is
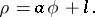 |
The spiral was studied by Archimedes (3rd century B.C.) and was named after him.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | E.H. Lockwood, "A book of curves" , Cambridge Univ. Press (1961) |
Archimedean spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Archimedean_spiral&oldid=16350