Normal family

of analytic functions in a domain

A family 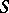of single-valued analytic functions 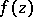of complex variables 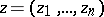in a domain 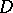in the space 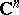, , 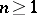such that from any sequence of functions in 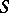one can extract a subsequence 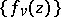that converges uniformly on compact subsets in 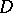to an analytic function or to infinity. Uniform convergence to infinity on compact subsets means, by definition, that for any compact set 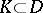and any 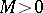one can find an 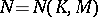such that 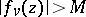for all , .

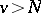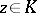A family 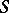is called a normal family at a point 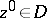if is normal in some ball with centre at 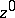. A family 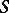is normal in 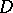if and only if it is normal at every point 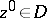. Every compact family of holomorphic functions is normal; the converse conclusion is false (see Compactness principle). If a family 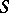of holomorphic functions in a domain 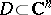has the property that all functions 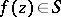omit two fixed values, then 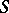is normal in 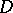(Montel's theorem). This criterion of normality considerably simplifies the investigation of analytic functions in a neighbourhood of an essential singular point (see also Picard theorem).

A normal family of meromorphic functions in a domain 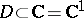is defined similarly: A family 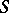of meromorphic functions in 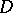is normal if from every sequence of functions in 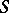one can extract a subsequence 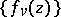that converges uniformly on compact subsets in 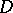to a meromorphic function or to infinity. By definition, converges uniformly on compact subsets in 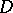to 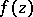(the case 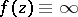is excluded) if for any compact set 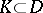and any 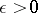there is an 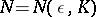and a disc 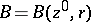of radius 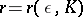with centre at some point 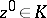such that for ,

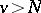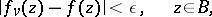when 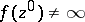, or

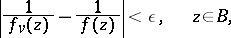when 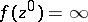. If a family of meromorphic functions in a domain 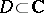has the property that all functions 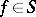omit three fixed values, then 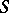is normal (Montel's theorem). A family 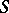of meromorphic functions is normal in a domain 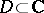if and only if

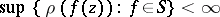on every compact set 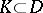, where

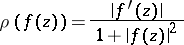is the so-called spherical derivative of .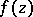

From the 1930s onwards great value was attached to the study of boundary properties of analytic functions (see also Cluster set, [3], [4]). A meromorphic function 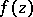in a simply-connected domain 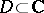is said to be a normal function in the domain 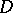if the family 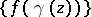is normal in 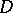, where 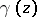ranges over the family of all conformal automorphisms of 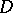. A function 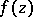is called normal in a multiply-connected domain if it is normal on the universal covering surface of 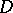. If a meromorphic functio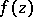n in 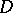omits three values, then 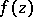is normal. For 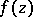, , 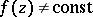to be normal in the unit disc 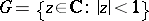it is necessary and sufficient that

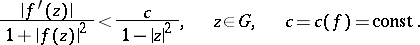For a normal meromorphic function 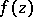in the unit disc 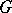the existence of an asymptotic value 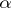at a boundary point implies that is a non-tangential boundary value (cf. Angular boundary value) of 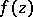at 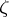. However, a meromorphic normal function in 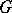need not have asymptotic values at all. On the other hand, if 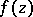is a holomorphic normal function in 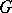, then non-tangential boundary values exist even on a set of points of the unit circle 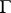that is dense in .

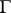References

[1]	P. Montel, "Leçons sur les familles normales de fonctions analytiques et leurs applications" , Gauthier-Villars (1927)
[2]	A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian)
[3]	E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6
[4]	A. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian)

Comments

Let , 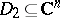be domains. A family 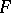of analytic mappings from 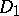to 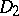is called normal if from any sequence of mappings in 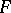one can either extract a subsequence 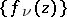that is uniformly convergent on compact subsets in 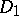to an analytic mapping from 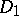to 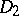, or a subsequence 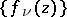with the property that for every compact sets 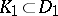, there is an 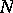such that 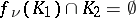for 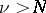, see [a1].

References

[a1]	S.G. Krantz, "Function theory of several complex variables" , Wiley (1982)
[a2]	O. Lehto, K.I. Virtanen, "Boundary behaviour and normal meromorphic functions" Acta Math. , 97 (1957) pp. 47–65