Montesinos-Nakanishi conjecture
From Encyclopedia of Mathematics
Any link can be reduced to a trivial link by a sequence of  -moves (that is, moves which add three half-twists into two parallel arcs of a link).
-moves (that is, moves which add three half-twists into two parallel arcs of a link).
The conjecture has been proved for links up to 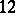 crossings,
crossings, 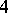 -bridge links and five-braid links except one family represented by the square of the centre of the
-bridge links and five-braid links except one family represented by the square of the centre of the  -braid group. This link, which can be reduced by
-braid group. This link, which can be reduced by  -moves to a
-moves to a  -crossings link, is the smallest known link for which the conjecture is open (as of 2001).
-crossings link, is the smallest known link for which the conjecture is open (as of 2001).
The conjecture has its stronger version that any  -tangle can be reduced by
-tangle can be reduced by  -moves to one of
-moves to one of 
 -tangles (with possible additional trivial components), where
-tangles (with possible additional trivial components), where 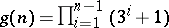 .
.
References
| [a1] | R. Kirby, "Problems in low-dimensional topology" W. Kazez (ed.) , Geometric Topology (Proc. Georgia Internat. Topol. Conf. 1993) , Stud. Adv. Math. , 2:2 , Amer. Math. Soc. /IP (1997) pp. 35–473 |
| [a2] | Q. Chen, "The  -move conjecture for -move conjecture for  -braids" , Knots in Hellas '98 (Proc. Internat. Conf. Knot Theory and Its Ramifications , Knots and Everything , 24 (2000) pp. 36–47 -braids" , Knots in Hellas '98 (Proc. Internat. Conf. Knot Theory and Its Ramifications , Knots and Everything , 24 (2000) pp. 36–47 |
| [a3] | J.H. Przytycki, T. Tsukamoto, "The fourth skein module and the Montesinos–Nakanishi conjecture for  -algebraic links" J. Knot Th. Ramifications , to appear (2001) -algebraic links" J. Knot Th. Ramifications , to appear (2001) |
| [a4] | H.R. Morton, "Problems" J.S. Birman (ed.) A. Libgober (ed.) , Braids (Santa Cruz, 1986) , Contemp. Math. , 78 , Amer. Math. Soc. (1988) pp. 557–574 |
How to Cite This Entry:
Montesinos-Nakanishi conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Montesinos-Nakanishi_conjecture&oldid=16341
Montesinos-Nakanishi conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Montesinos-Nakanishi_conjecture&oldid=16341
This article was adapted from an original article by Jozef Przytycki (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article