Specht module
Let  and suppose
and suppose  is a (proper) partition of
is a (proper) partition of  . This means that
. This means that  , where each
, where each  and
and  . If
. If  is maximal with
is maximal with  , then one says that
, then one says that  is a partition of
is a partition of  into
into  parts.
parts.
A 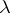 -tableau (sometimes called a Young tableau associated with
-tableau (sometimes called a Young tableau associated with 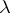 ) is an array consisting of the numbers
) is an array consisting of the numbers 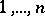 listed in
listed in  rows with exactly
rows with exactly  numbers occurring in the
numbers occurring in the 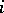 th row,
th row, 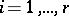 . If, for instance,
. If, for instance,  and
and 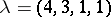 , then the following arrays are examples of
, then the following arrays are examples of  -tableaux:
-tableaux:
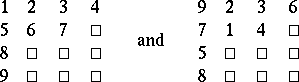 |
One says that two 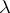 -tableaux are equivalent if for each
-tableaux are equivalent if for each 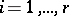 the two sets of numbers in the
the two sets of numbers in the 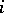 th rows of the two arrays coincide. Clearly, the two
th rows of the two arrays coincide. Clearly, the two 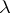 -tableaux above are not equivalent. The equivalence classes with respect to this relation are called
-tableaux above are not equivalent. The equivalence classes with respect to this relation are called 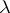 -tabloids. If
-tabloids. If 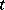 is a
is a  -tableau, one usually denotes the
-tableau, one usually denotes the 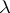 -tabloid by
-tabloid by 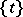 . As examples, for
. As examples, for 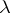 as above one has
as above one has
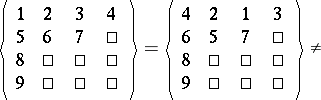 |
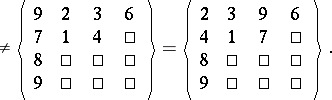 |
Suppose 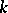 is a field. Denote by
is a field. Denote by 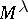 the vector space over
the vector space over  with basis equal to the set of
with basis equal to the set of 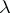 -tabloids. Then the symmetric group
-tabloids. Then the symmetric group 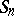 on
on  letters (cf. also Symmetric group) acts on
letters (cf. also Symmetric group) acts on 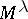 (or, more precisely,
(or, more precisely, 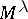 is a
is a 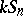 -module) in a natural way. Indeed, if
-module) in a natural way. Indeed, if 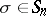 and
and 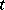 is a
is a 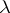 -tableau, then
-tableau, then 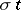 is the
is the 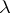 -tableau obtained from
-tableau obtained from 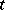 by replacing each number
by replacing each number 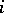 by
by 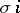 . If one uses the usual cycle presentation of elements in
. If one uses the usual cycle presentation of elements in  , then, e.g., for
, then, e.g., for 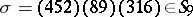 one has
one has
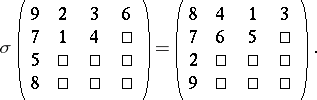 |
This action clearly induces an action of  on
on 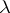 -tabloids and this gives the desired module structure on
-tabloids and this gives the desired module structure on  .
.
If, again, 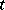 is a
is a 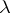 -tableau, then one sets
-tableau, then one sets
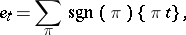 |
where the sum runs over the 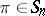 that leave the set of numbers in each column in
that leave the set of numbers in each column in 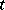 stable. Here,
stable. Here, 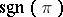 is the sign of
is the sign of 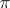 .
.
The Specht module associated to 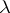 is defined as the submodule
is defined as the submodule
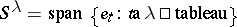 |
of  . Clearly,
. Clearly, 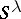 is invariant under the action of
is invariant under the action of 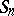 . (In fact,
. (In fact, 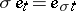 for all
for all  and all
and all 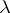 -tableau
-tableau 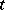 .)
.)
Specht modules were introduced in 1935 by W. Specht [a5]. Their importance in the representation theory for symmetric groups (cf. also Representation of the symmetric groups) comes from the fact that when 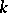 contains
contains 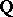 , then each
, then each 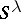 is a simple
is a simple  -module. Moreover, the set
-module. Moreover, the set
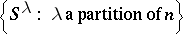 |
is a full set of simple 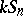 -modules.
-modules.
When the characteristic of 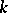 is
is 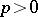 , then the Specht modules are no longer always simple. However, they still play an important role in the classification of simple
, then the Specht modules are no longer always simple. However, they still play an important role in the classification of simple  -modules. Namely, it turns out that when
-modules. Namely, it turns out that when 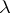 is
is 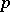 -regular (i.e. no
-regular (i.e. no 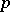 parts of
parts of 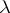 are equal), then
are equal), then 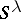 has a unique simple quotient
has a unique simple quotient 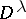 and the set
and the set
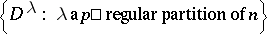 |
constitutes a full set of simple 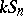 -modules. It is a major open problem (1999) to determine the dimensions of these modules.
-modules. It is a major open problem (1999) to determine the dimensions of these modules.
It is possible to give a (characteristic-free) natural basis for 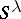 . This is sometimes referred to as the Specht basis. In the notation above, it is given by
. This is sometimes referred to as the Specht basis. In the notation above, it is given by
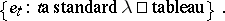 |
Here, a 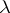 -tableau
-tableau 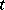 is called standard if the numbers occurring in
is called standard if the numbers occurring in 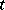 are increasing along each row and down each column.
are increasing along each row and down each column.
An immediate consequence is that the dimension of 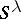 equals the number of standard
equals the number of standard 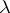 -tableaux. For various formulas for this number (as well as many further properties of Specht modules) see [a2] and [a3].
-tableaux. For various formulas for this number (as well as many further properties of Specht modules) see [a2] and [a3].
The representation theory for symmetric groups is intimately related to the corresponding theory for general linear groups (Schur duality). Under this correspondence, Specht modules play the same role for 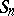 as do the Weyl modules for
as do the Weyl modules for 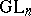 , see e.g. [a1] and Weyl module. For a recent result exploring this correspondence in characteristic
, see e.g. [a1] and Weyl module. For a recent result exploring this correspondence in characteristic 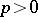 , see [a4].
, see [a4].
References
| [a1] | J.A. Green, "Polynomial representations of 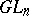 " , Lecture Notes Math. , 830 , Springer (1980) " , Lecture Notes Math. , 830 , Springer (1980) |
| [a2] | G.D. James, "The representation theory of the symmetric groups" , Lecture Notes Math. , 682 , Springer (1978) |
| [a3] | G.D. James, A. Kerber, "The representation theory of the symmetric group" , Encycl. Math. Appl. , 16 , Addison-Wesley (1981) |
| [a4] | O. Mathieu, "On the dimension of some modular irreducible representations of the symmetric group" Lett. Math. Phys. , 38 (1996) pp. 23–32 |
| [a5] | W. Specht, "Die irreduziblen Darstellungen der symmetrischen Gruppe" Math. Z. , 39 (1935) pp. 696–711 |
Specht module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Specht_module&oldid=16338