A problem in the calculus of variations in which an extremum of a functional is attained on a polygonal extremal. A polygonal extremal is a piecewise-smooth solution of the Euler equation satisfying certain additional necessary conditions at the vertices. The actual form of these conditions depends on the type of the discontinuous variational problem. Thus, in a first-order discontinuous variational problem the polygonal extremal is found by making the usual assumptions of continuity and continuous differentiability of the integrand. For the simplest kind of functional
 | (1) |
it is necessary that the Weierstrass–Erdmann conditions
 | (2) |
 | (3) |
be fulfilled at a corner 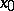 of the polygonal extremal. When
of the polygonal extremal. When 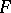 depends on
depends on  unknown functions, that is, when
unknown functions, that is, when 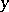 in (1) is an
in (1) is an  -dimensional vector
-dimensional vector 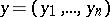 , then the Weierstrass–Erdmann corner conditions analogous to (2), (3) are
, then the Weierstrass–Erdmann corner conditions analogous to (2), (3) are
 | (4) |
 | (5) |
For problems on conditional extrema in which the integrand depends on  unknown functions and when there are
unknown functions and when there are 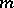 differential constraints given as equations (see Bolza problem), the Weierstrass–Erdmann conditions have to be expressed in terms of the Lagrange function
differential constraints given as equations (see Bolza problem), the Weierstrass–Erdmann conditions have to be expressed in terms of the Lagrange function 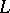 and have the same form as (4), (5), but with
and have the same form as (4), (5), but with 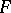 replaced by
replaced by 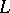 .
.
In terms of the theory of optimal control the necessary conditions at a corner of a polygonal extremal require the continuity of the conjugate variables and of the Hamilton function at the points of discontinuity of the optimal control. As is implied by the Pontryagin maximum principle, these conditions are automatically fulfilled if along a polygonal extremal the control is determined by the condition that the Hamilton function has a maximum.
In a second-order discontinuous variational problem the integrand is discontinuous. Let, for example, 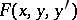 have a discontinuity along the line
have a discontinuity along the line 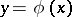 , so that
, so that 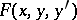 is equal to
is equal to  and
and 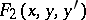 , respectively, along one side or the other of
, respectively, along one side or the other of 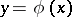 . Then, if the optimal solution exists, it is achieved on a polygonal extremal which has a corner at
. Then, if the optimal solution exists, it is achieved on a polygonal extremal which has a corner at 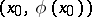 and one obtains, instead of the functional (1), the functional
and one obtains, instead of the functional (1), the functional
 | (6) |
A variation of the functional (6) reduces to a variation of the functionals 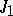 and
and 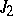 on matching curves which have moving right and left end points sliding along
on matching curves which have moving right and left end points sliding along 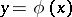 . In order that a minimum for the functional (6) is attained on a polygonal extremal, it is necessary that at a corner
. In order that a minimum for the functional (6) is attained on a polygonal extremal, it is necessary that at a corner 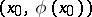 one has
one has
 | (7) |
When 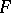 depends on
depends on  unknown functions
unknown functions  and the surface of discontinuity of
and the surface of discontinuity of 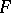 is given in the form
is given in the form
 | (8) |
the necessary conditions at a corner of a polygonal extremal which is on the surface (8) take the form
 | (9) |
The necessary conditions (7), (9) are insufficient for computing the arbitrary constants determining the polygonal extremal — it is a particular solution of the Euler equation satisfying the boundary conditions. In fact, the equations (9) give  necessary conditions which, together with the
necessary conditions which, together with the 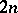 boundary conditions, the
boundary conditions, the  conditions for the polygonal extremal to be joined continuously at a corner and equation (8) give
conditions for the polygonal extremal to be joined continuously at a corner and equation (8) give 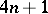 conditions, so that it is possible to determine the
conditions, so that it is possible to determine the  -coordinate
-coordinate 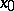 of the vertex and
of the vertex and 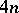 arbitrary constants,
arbitrary constants, 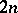 for each of the extremals coming up to the different sides of the surface (8).
for each of the extremals coming up to the different sides of the surface (8).
References
| [1] | N.M. Gyunter, "A course in the calculus of variations" , Leningrad-Moscow (1941) (In Russian) |
| [2] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [3] | L.S. Pontryagin, V.G. Boltayanskii, R.V. Gamkrelidze, E.F. Mishchenko, "The mathematical theory of optimal processes" , Wiley (1962) (Translated from Russian) |
References
| [a1] | W.H. Fleming, R.W. Rishel, "Deterministic and stochastic optimal control" , Springer (1975) |
| [a2] | A.E. Bryson, Y.-C. Ho, "Applied optimal control" , Ginn & Waltham (1969) |
How to Cite This Entry:
Discontinuous variational problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discontinuous_variational_problem&oldid=16324
This article was adapted from an original article by I.B. Vapnyarskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article


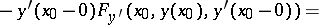
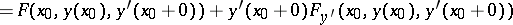
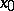 of the polygonal extremal. When
of the polygonal extremal. When 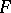 depends on
depends on  unknown functions, that is, when
unknown functions, that is, when 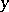 in (1) is an
in (1) is an  -dimensional vector
-dimensional vector 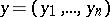 , then the Weierstrass–Erdmann corner conditions analogous to (2), (3) are
, then the Weierstrass–Erdmann corner conditions analogous to (2), (3) are


 unknown functions and when there are
unknown functions and when there are 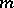 differential constraints given as equations (see Bolza problem), the Weierstrass–Erdmann conditions have to be expressed in terms of the Lagrange function
differential constraints given as equations (see Bolza problem), the Weierstrass–Erdmann conditions have to be expressed in terms of the Lagrange function 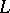 and have the same form as (4), (5), but with
and have the same form as (4), (5), but with 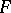 replaced by
replaced by 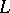 .
.
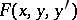 have a discontinuity along the line
have a discontinuity along the line 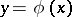 , so that
, so that 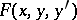 is equal to
is equal to  and
and 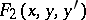 , respectively, along one side or the other of
, respectively, along one side or the other of 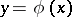 . Then, if the optimal solution exists, it is achieved on a polygonal extremal which has a corner at
. Then, if the optimal solution exists, it is achieved on a polygonal extremal which has a corner at 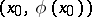 and one obtains, instead of the functional (1), the functional
and one obtains, instead of the functional (1), the functional

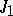 and
and 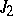 on matching curves which have moving right and left end points sliding along
on matching curves which have moving right and left end points sliding along 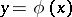 . In order that a minimum for the functional (6) is attained on a polygonal extremal, it is necessary that at a corner
. In order that a minimum for the functional (6) is attained on a polygonal extremal, it is necessary that at a corner 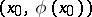 one has
one has

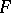 depends on
depends on  unknown functions
unknown functions  and the surface of discontinuity of
and the surface of discontinuity of 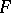 is given in the form
is given in the form


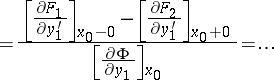
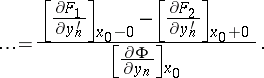
 necessary conditions which, together with the
necessary conditions which, together with the 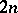 boundary conditions, the
boundary conditions, the  conditions for the polygonal extremal to be joined continuously at a corner and equation (8) give
conditions for the polygonal extremal to be joined continuously at a corner and equation (8) give 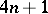 conditions, so that it is possible to determine the
conditions, so that it is possible to determine the  -coordinate
-coordinate 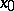 of the vertex and
of the vertex and 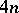 arbitrary constants,
arbitrary constants, 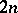 for each of the extremals coming up to the different sides of the surface (8).
for each of the extremals coming up to the different sides of the surface (8).