Divisor class group
The quotient group of the group  of divisorial ideals (cf. Divisorial ideal) of a Krull ring
of divisorial ideals (cf. Divisorial ideal) of a Krull ring  by the subgroup
by the subgroup 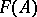 consisting of the principal ideals. The divisor class group is Abelian and is usually denoted by
consisting of the principal ideals. The divisor class group is Abelian and is usually denoted by  . The group
. The group  is generated by the classes of the prime ideals of height 1 in
is generated by the classes of the prime ideals of height 1 in  (cf. Height of an ideal).
(cf. Height of an ideal).
In a sense, the divisor class group measures the divergence from uniqueness of the factorization of elements of  into irreducible factors. Thus, a factorial ring has trivial divisor class group.
into irreducible factors. Thus, a factorial ring has trivial divisor class group.
Let  be a homomorphism of Krull rings; then, under certain additional assumptions (for instance, when
be a homomorphism of Krull rings; then, under certain additional assumptions (for instance, when  is an integral or flat extension of
is an integral or flat extension of 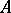 ), there is a canonical homomorphism
), there is a canonical homomorphism 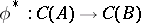 of divisor class groups. If
of divisor class groups. If 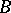 is the localization of
is the localization of 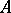 with respect to a multiplicative system
with respect to a multiplicative system 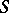 (cf. Localization in a commutative algebra), then
(cf. Localization in a commutative algebra), then 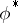 is surjective and the kernel of
is surjective and the kernel of 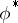 is generated by the divisorial prime ideals of
is generated by the divisorial prime ideals of 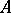 that meet
that meet  (Nagata's theorem). If
(Nagata's theorem). If 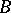 is the ring of polynomials over
is the ring of polynomials over 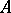 , then the canonical homomorphism
, then the canonical homomorphism 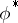 is bijective (this is a generalization of Gauss' theorem stating that the ring of polynomials over a field is factorial). In the more general case where
is bijective (this is a generalization of Gauss' theorem stating that the ring of polynomials over a field is factorial). In the more general case where 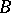 is the symmetric Noetherian algebra of an
is the symmetric Noetherian algebra of an 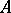 -module
-module 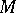 , the canonical homomorphism
, the canonical homomorphism 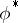 is bijective provided that all symmetric powers
is bijective provided that all symmetric powers 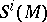 are reflexive. If
are reflexive. If  is the ring of formal power series over
is the ring of formal power series over 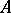 , then
, then 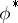 is injective (and even left invertible), but not bijective, in general.
is injective (and even left invertible), but not bijective, in general.
The subgroup of  generated by the invertible ideals is isomorphic to the Picard group
generated by the invertible ideals is isomorphic to the Picard group 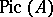 of
of 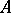 , and the functorial properties of
, and the functorial properties of 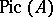 and
and 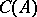 are compatible. Thus, if
are compatible. Thus, if 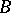 is a faithfully flat extension of a ring
is a faithfully flat extension of a ring  and
and 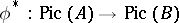 is injective, then
is injective, then 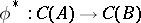 is also injective. In particular, if the completion
is also injective. In particular, if the completion 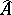 of a local ring
of a local ring 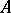 is factorial, then
is factorial, then 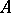 is also factorial (Mori's theorem).
is also factorial (Mori's theorem).
Let  be a normal Noetherian ring. The group
be a normal Noetherian ring. The group 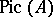 coincides with
coincides with 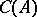 if and only if
if and only if 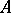 is locally a factorial ring, that is, if all the local rings
is locally a factorial ring, that is, if all the local rings 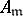 are factorial (for instance, when
are factorial (for instance, when 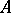 is regular). More exactly, if
is regular). More exactly, if 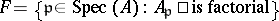 , then
, then 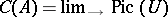 , where
, where 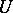 runs over the system of open subschemes of
runs over the system of open subschemes of 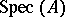 containing
containing 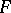 . This allows one to define the divisor class group of a normal scheme [5] — the Weil divisor class group (see Divisor).
. This allows one to define the divisor class group of a normal scheme [5] — the Weil divisor class group (see Divisor).
Divisor class groups were first studied for rings of algebraic numbers, and the earliest results concerning the finiteness of these groups were obtained by E. Kummer. There is a close connection between the properties of the divisor class group and number-theoretical problems, for instance, Fermat's theorem. Tables of orders of divisor class groups of certain rings of algebraic numbers are provided in [1].
In full generality, the theory of divisor class groups was obtained by W. Krull; P. Samuel studied the functorial character of divisor class groups and proposed some methods for computing them (for example, the method of descent). Other approaches to the study of the divisor class group are based on comparison with the Picard group, and cohomological and algebraic-geometrical methods are applied as well.
Every Abelian group occurs as a divisor class group.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [3] | P. Samuel, "Classes de diviseurs et dérivées logarithmiques" Topology , 3 (1964) pp. 81–96 |
| [4] | R.M. Fossum, "The divisor class group of a Krull domain" , Springer (1973) |
| [5] | A. Grothendieck, J. Dieudonné, "Eléments de géometry algébrique IV" Publ. Math. IHES , 32 (1967) |
Comments
Cf. also Class field theory for the relation between the divisor class group of a ring of algebraic integers and Abelian field extensions.
Divisor class group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Divisor_class_group&oldid=16323