Locally integrable function

at a point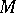

A function that is integrable in some sense or other in a neighbourhood of 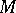. If a real-valued function 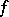, defined on the interval 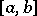, is the pointwise finite derivative of a function 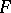, real-valued and defined on this interval, then 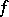is locally Lebesgue integrable at the points of an open everywhere-dense set on 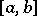. In the two-dimensional case (see [2]) there is a real-valued function 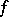, defined on the square 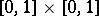, that is the pointwise finite mixed derivative in either order 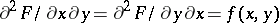and that is not locally Lebesgue integrable at any point of the square.

References

[1]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)
[2]	G.P. Tolstov, "On the curvilinear and iterated integral" Trudy Mat. Inst. Steklov. , 35 (1950) pp. 1–101 (In Russian)