Permutation

of elements

A finite sequence of length in which all the elements are different, i.e. a permutation is an arrangement of elements without repetition. The number of permutations is .

Usually, one takes as the elements to be permuted the elements of the set ; a one-to-one mapping of onto itself defines the permutation . The mapping is also called a substitution of . Many problems related to the enumeration of permutations are formulated in terms of substitutions, such as, for example, the enumeration of permutations with various restrictions on the positions of the permuted elements (cf. e.g. [1], [2]). A permutation 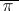can be regarded as an ordered set consisting of elements if one assumes that 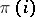precedes , .

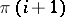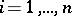Examples. 1) The pair 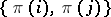forms an inversion in 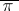if for ; if 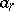is the number of permutations of elements with inversions, then

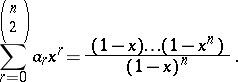2) If 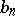is the number of permutations 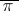consisting of elements such that 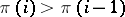for 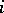even and for 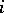odd, then

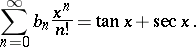Often a permutation is defined to be a bijective mapping of a finite set onto itself, i.e. a substitution (cf. also Permutation of a set).

References

[1]	V.N. Sachkov, "Combinatorial methods in discrete mathematics" , Moscow (1977) (In Russian)
[2]	J. Riordan, "An introduction to combinational analysis" , Wiley (1958)

Comments

See also Permutation group.