Signature
The signature of an algebraic system is the collection of relations and operations on the basic set of the given algebraic system together with an indication of their arity. An algebraic system (a universal algebra) with signature  is also called an
is also called an  -system (respectively,
-system (respectively,  -algebra).
-algebra).
The signature of a quadratic, or symmetric bilinear, form over an ordered field is a pair of non-negative integers 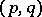 , where
, where 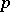 is the positive and
is the positive and 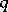 the negative index of inertia of the given form (see Law of inertia; Quadratic form). Sometimes the number
the negative index of inertia of the given form (see Law of inertia; Quadratic form). Sometimes the number 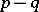 is called the signature of the form.
is called the signature of the form.
O.A. Ivanova
The signature of a manifold 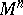 is the signature of the quadratic form
is the signature of the quadratic form
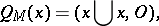 |
where 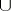 is the cohomology cup-product and
is the cohomology cup-product and 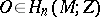 is the fundamental class. The manifold is assumed to be compact, orientable and of dimension
is the fundamental class. The manifold is assumed to be compact, orientable and of dimension 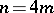 . The signature is denoted by
. The signature is denoted by 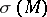 .
.
If 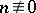
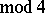 , one sets
, one sets 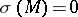 . The signature has the following properties:
. The signature has the following properties:
a) 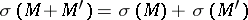 ;
;
b) 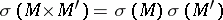 ;
;
c) 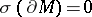 .
.
The signature of a manifold can be represented as a linear function of its Pontryagin numbers (cf. Pontryagin number; [2]). For the representation of the signature as the index of a differential operator see Index formulas.
References
| [1] | A. Dold, "Lectures on algebraic topology" , Springer (1980) |
| [2] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) |
M.I. Voitsekhovskii
Comments
Let 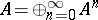 be a commutative graded algebra over a commutative ring
be a commutative graded algebra over a commutative ring 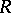 with unit. Let
with unit. Let 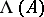 denote the group of all elements
denote the group of all elements 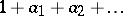 ,
,  , under the obvious multiplication of such expressions:
, under the obvious multiplication of such expressions:
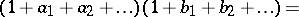 |
 |
A sequence 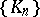 of polynomials
of polynomials 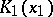 ,
, 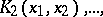 with coefficients in
with coefficients in 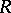 is called a multiplicative sequence of polynomials if each
is called a multiplicative sequence of polynomials if each 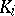 is homogeneous of degree
is homogeneous of degree 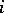 and if for each
and if for each 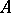 the mapping
the mapping 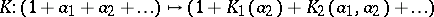 defines a group homomorphism from
defines a group homomorphism from  to
to 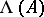 . Given a power series
. Given a power series 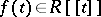 with constant term
with constant term 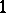 , there is precisely one multiplicative sequence
, there is precisely one multiplicative sequence 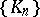 over
over 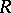 such that
such that 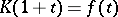 . This multiplicative sequence is called the multiplicative sequence defined by the power series
. This multiplicative sequence is called the multiplicative sequence defined by the power series 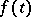 .
.
Now, let 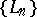 be the multiplicative sequence defined by the power series
be the multiplicative sequence defined by the power series
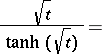 |
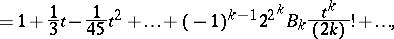 |
where 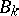 is the
is the 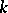 -th Bernoulli number (cf. Bernoulli numbers). The
-th Bernoulli number (cf. Bernoulli numbers). The  -genus of a manifold
-genus of a manifold 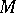 of dimension
of dimension 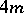 is defined by
is defined by
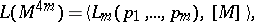 |
where 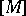 is the fundamental homology class of
is the fundamental homology class of 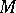 and
and 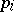 is the
is the 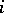 -th Pontryagin class. One sets
-th Pontryagin class. One sets 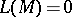 if the dimension of
if the dimension of 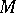 is not a multiple of
is not a multiple of 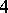 . The Hirzebruch signature theorem now says that the
. The Hirzebruch signature theorem now says that the 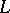 -genus of a manifold is equal to its signature [2], §19.
-genus of a manifold is equal to its signature [2], §19.
In some of the older literature the signature of a manifold is referred to as the index of a manifold.
Signature. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Signature&oldid=16291