Discrete distribution

A probability distribution (concentrated) on a finite or countably infinite set of points of a sampling space . More exactly, let be the sample points and let

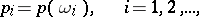(1)

be numbers satisfying the conditions

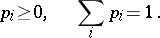(2)

Relations (1) and (2) fully define a discrete distribution on the space , since the probability measure of any set is defined by the equation

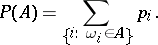Accordingly, the distribution of a random variable is said to be discrete if it assumes, with probability one, a finite or a countably infinite number of distinct values with probabilities . In the case of a distribution on the real line, the distribution function 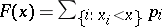has jumps at the points 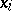equal to 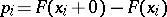, and is constant in the intervals 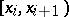. The following discrete distributions occur most frequently: the binomial distribution, the geometric distribution, the hypergeometric distribution, the negative binomial distribution, the multinomial distribution, and the Poisson distribution.

Comments

A word of caution. In the Russian literature, 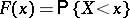, whereas in Western literature 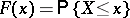. So the distribution functions are slightly different: left continuous in the Russian literature, and right continuous in the Western literature.