Continuum, cardinality of the
The cardinal number 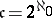 , i.e. the cardinality of the set of all subsets of the natural numbers. The following sets have the cardinality of the continuum: 1) the set
, i.e. the cardinality of the set of all subsets of the natural numbers. The following sets have the cardinality of the continuum: 1) the set 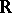 of all real numbers; 2) the set of all points in the interval
of all real numbers; 2) the set of all points in the interval 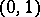 ; 3) the set of all irrational numbers in this interval; 4) the set of all points of the space
; 3) the set of all irrational numbers in this interval; 4) the set of all points of the space  , where
, where  is a positive integer; 5) the set of all transcendental numbers; and 6) the set of all continuous functions of a real variable. The cardinality of the continuum cannot be represented as a countable sum of smaller cardinal numbers. For any cardinal number
is a positive integer; 5) the set of all transcendental numbers; and 6) the set of all continuous functions of a real variable. The cardinality of the continuum cannot be represented as a countable sum of smaller cardinal numbers. For any cardinal number 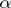 such that
such that 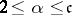 ,
,
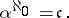 |
In particular,
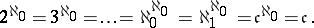 |
The continuum hypothesis states that the cardinality of the continuum is the first uncountable cardinal number, that is,
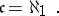 |
References
| [1] | K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968) |
Continuum, cardinality of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuum,_cardinality_of_the&oldid=16271