D-module

The theory of 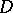-modules is an algebraic formalism of the theory of linear partial differential equations (cf. Linear partial differential equation). It is concerned with modules over rings of differential operators (cf. Module) and has been developed by I.N. Bernstein, J.-E. Björk, M. Kashiwara, T. Kawai, B. Malgrange, Z. Mebkhout, and others. Lately the theory of 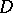-modules has found applications in several parts of mathematics, e.g., cohomology of singular spaces, Hodge structure on intersection cohomology, singularity theory (cf. Singularities of differentiable mappings), Gauss–Manin connection, representation theory, and Kazhdan–Lusztig conjectures. Two survey articles on the theory of 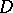-modules are [a10] and [a14]. There is a very elegant theory of 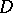-modules in case the underlying manifolds are algebraic (cf. [a4]). An illuminating account of the analytic theory may be found in [a15] (cf. also [a2], [a3]). A powerful technique is to work microlocally and introduce microdifferential operators (cf. [a7], [a9], [a18]). However, microlocal results related to 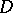-modules will not be presented below.

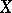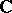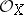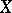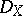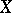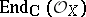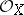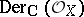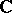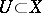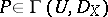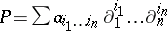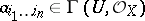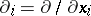Henceforth, let denote a complex analytic manifold (cf. Complex manifold) or a smooth algebraic variety over . Denote by the structure sheaf of . The sheaf of differential operators on is the subsheaf of generated by and , the sheaf of -linear derivations. Hence on a chart with coordinates an element can be written as a finite sum , where and . In particular in the algebraic case, being a bit more general, if 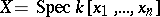, where is a field of characteristic zero, then 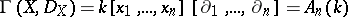is the -th Weyl algebra over . 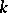The sheaf 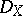is a coherent sheaf of non-commutative left and right Noetherian rings (cf. [a3]). The structure sheaf 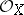becomes in a natural way a coherent left 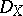-module. More generally, let 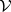be a vector bundle on 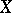with an integrable connection . 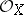The -structure on 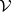extends to a left 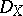-module structure by putting 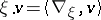for all local sections 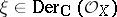, 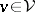. Conversely, each left 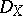-module whose underlying 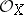-module is coherent is of this form.

Usually one considers only left 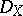-modules. This is harmless as one can freely exchange left and right 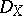-modules. Namely, the 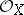-module 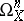(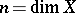) of highest-order differential forms on 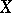carries a natural structure of a coherent right 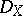-module: for all 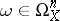, 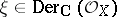one puts 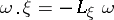, where 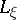denotes the Lie derivative with respect to 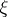. Then 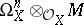has a right 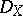-structure for any left 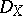-module 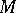and 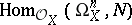has a left 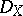-structure for any right 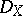-module .

Let 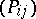be a -matrix with coefficients 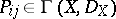and consider the left 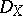-linear mapping , defined by letting the matrix 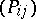act from the right on 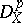. Then 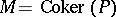is a coherent left 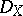-module. Clearly, 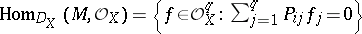. Thus, holomorphic solutions of the linear system 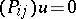can be interpreted as elements of the 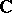-vector space 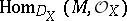, and vice versa. This leads one to consider the derived solution complex 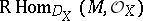for any left 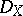-module 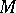. Identifying 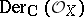with a subsheaf of 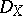enables one to construct the complex 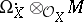. It is denoted by 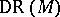and is called the de Rham complex of .

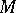Operations on 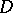-modules.

For an adequate setting of the theory of 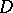-modules the machinery of derived categories and derived functors is indispensable. Denote by 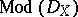(respectively, 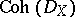) the category of left (respectively, coherent) 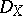-modules. Denote by 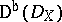the derived category of bounded complexes of left 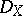-modules. Let 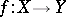be a holomorphic mapping between complex analytic (or smooth algebraic) manifolds. Let 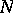be a left 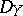-module. The 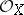-module 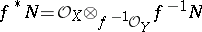carries a natural left 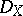-structure. One puts 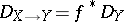. This is a left 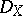-, right 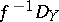-bimodule. The inverse image functor is then given by

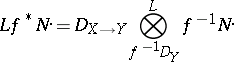for all .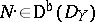

Using the left-right principle yields a left 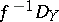-, right 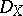-bimodule 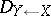. The direct image functor 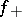is then defined as

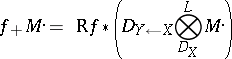for all .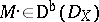

Frequently one uses 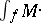to denote the direct image. In the algebraic category one has the following result: If 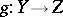is another morphism, then 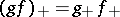. In the analytic category the same holds if 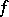is proper.

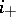In case of a closed imbedding the direct image is an exact functor from 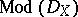to 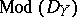which preserves coherency. In fact one has the following (Kashiwara's equivalence): 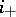establishes an equivalence between and the category of coherent -modules with support contained in 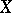. In case of a submersion 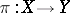and a 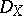-module 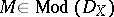the complex of relative differential forms gives rise to the relative de Rham complex 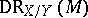. The direct image is then 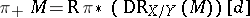, where .

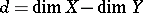Let 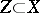be a closed subvariety defined by an ideal 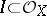. For any left 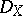-module 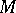define . It is the -submodule of 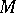consisting of the sections annihilated by some power of 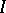. It is an analogue of the usual functor "sections with support" . Its 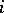-th derived functor is often denoted by 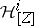. Of course, in the algebraic category .

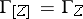Holonomic 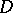-modules.

The sheaf 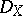is filtered by the order of a differential operator. The associated graded 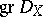may be identified with the sheaf of holomorphic functions on 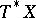which are polynomial in the fibres. Since a coherent 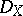-module 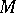is locally of finite presentation, it carries locally a so-called good filtration; cf. Filtered module. This gives rise, at least locally, to a coherent ideal in 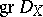, namely the annihilator of 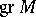. It turns out that its radical does not depend on the filtration, so patches together and yields a radical homogeneous ideal in 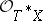. Its locus defines a closed conic subvariety 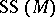of 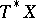, called the singular support or the characteristic variety of 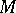. Closely related is the characteristic cycle 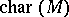. This is the formal linear combination of the irreducible components of 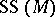counted with their multiplicities.

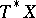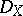The cotangent bundle has the structure of a symplectic manifold. The following basic result was proved by microlocal analysis by Kashiwara, Kawai and M. Sato at the conference in Katata, 1971: The characteristic variety of a coherent -module 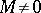is involutive. An algebraic proof was given by O. Gabber [a5]. Instead of "involutive" one uses also "co-isotropic characteristic variety of a D-moduleco-isotropic" . 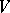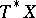Recall that an involutive subvariety of has 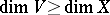. If equality holds, 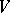is a Lagrangian manifold. Now a non-zero 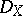-module is said to be holonomic if it is coherent and its characteristic variety is Lagrangian. The zero module is also defined to be holonomic. For instance, any vector bundle 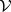with an integrable connection is holonomic since its characteristic variety is the zero-section of . Furthermore, its the Rham complex 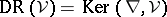is a local system on .

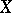The characteristic variety of a holonomic 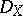-module 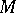is of the form 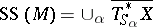, wher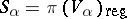e , the 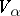are the irreducible components of 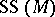and 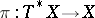denotes the projection. An important property of holonomic modules is the following result of Kashiwara (see, e.g., [a7]), which says: The de Rham complex 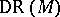of a holonomic 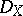-module 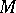is constructible. Recall that a sheaf 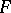of vector spaces on 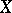is called constructible if there exists a stratification 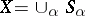such that the restriction of 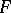to each stratum 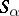is a local system. Denote by the derived category of bounded complexes of sheaves of 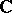-vector spaces with constructible cohomology. Also the solution complex of a holonomic 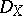-module 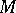is constructible since it is isomorphic to the Verdier dual (cf. Derived category) of 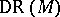. (Cf. [a12].)

The Bernstein–Sato polynomial.

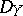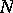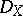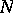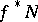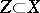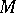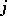The inverse image of a coherent -module is not necessarily a coherent -module. However, if one assumes that is holonomic then is also holonomic and, in particular, coherent. Moreover, for each closed subvariety and for every holonomic -module the local cohomology is holonomic for all . Closely related to this is the following statement, which has become one of the cornerstones of the theory of 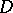-modules. Let 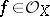. There exists a non-zero polynomial 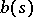and 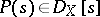such that .

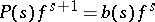The monic polynomial of lowest degree which satisfies this is called the Bernstein–Sato polynomial or the -function 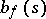of . This result has been proved by Bernstein in the algebraic case and by Björk in the analytic case. Kashiwara proved that the roots of the 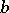-function are rational numbers. If 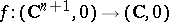is a germ of a holomorphic function, Malgrange proved that the set 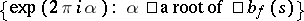contains all the eigen values of the monodromy in all dimensions. There is also the work of D. Barlet; for instance, in [a1] he proves that the roots of the 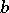-function produce poles of the meromorphic continuation of 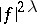. More precisely, if 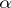is a root of 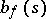, then there exists an integer 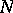such that 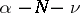is a pole of 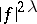for every non-negative integer . Finally, the 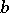-function is related to the vanishing cycle functor of P. Deligne. For this see, e.g., [a11].

Regular holonomic 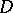-modules.

The notion of regular singularities is classical in the one-dimensional case (cf. Regular singular point). Recall that a differential operator , , 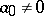defined in a neighbourhood of 0 in 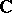is said to have a regular singularity at if the multi-valued solutions of the differential equation 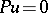have a moderate growth. By a classical theorem of Fuchs this is equivalent to 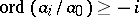for all 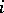. An equivalent formulation due to Malgrange is that 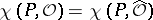, where 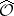is the formal completion of 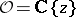. The index 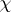is defined as 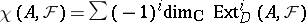. See, for instance, [a4], Chapts. 3, 4. The notion of regularity has been generalized to higher dimensions by Deligne. Generalizations to 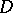-modules are due to Kashiwara, Mebkhout, Oshima, and J.-P. Ramis. There are various equivalent definitions of regularity in the literature, of which the following is given here: A holonomic 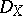-module is said to have regular singularities if 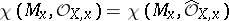for all .

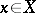Note that in the algebraic category one requires that the points "at infinity" are regular. (Cf. [a4], Chapt. 7 for a definition due to Bernstein.) Let 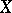be a smooth algebraic variety and let 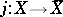be a smooth completion. Let 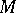be a holonomic 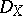-module. Then 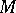is regular if and only if 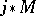is regular. Via GAGA this amounts to the regularity of 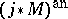on 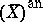, the underlying complex analytic manifold. In the algebraic case regularity is preserved under direct or inverse images. In the analytic case the direct image functor preserves regular holonomicity under proper mappings (cf. [a9]). See [a6] for a result on the non-proper case. The inverse image functor preserves regularity. For any closed subspace 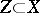and any 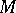a regular holonomic 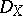-module 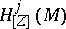has regular singularities for all .

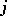The Riemann–Hilbert correspondence.

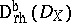It asserts that: The de Rham functor establishes an equivalence of categories between and 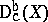. Here 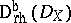denotes the derived category of bounded complexes of 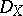-modules with regular holonomic cohomology. This result is independently due to Kashiwara, Kawai (cf. [a8], [a9]) and Mebkhout [a13]. It is tacitly assumed here that 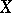is analytic. In the algebraic case 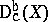has to replaced by 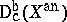(cf. [a4]). This correspondence is one of the highlights in the theory of 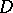-modules. It establishes a bridge between analytic objects (regular holonomic 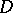-modules) and geometric ones (constructible sheaves).

Perverse sheaves.

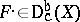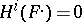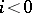A constructible sheaf is called a perverse sheaf if 1) for and 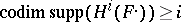; 2) the Verdier dual 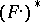also satisfies 1). Then the Riemann–Hilbert correspondence induces an equivalence between the category of regular holonomic 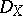-modules and the category of perverse sheaves on 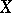. An example of a perverse sheaf is the intersection cohomology complex 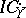, where 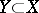is a closed analytic subspace. In case 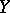is projective it has been conjectured that the intersection cohomology groups 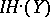carry a pure Hodge structure. Using the framework of 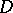-modules this has been confirmed by M. Saito (cf. [a16], [a17]). He also gives an analytic proof of the decomposition theorem of Beilinson, Bernstein, Deligne, and Gabber.

References

[a1]	D. Barlet, "Monodromie et pôles du prolongement méromorphe de 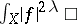" Bull. Soc. Math. France , 114 (1986) pp. 247–269
[a2]	J.-E. Björk, "Analytic 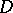-modules" , Kluwer (1993)
[a3]	J.-E. Björk, "Rings of differential operators" , North-Holland (1979)
[a4]	A. Borel, et al., "Algebraic 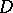-modules" , Acad. Press (1987)
[a5]	O. Gabber, "The integrability of the characteristic variety" Amer. J. Math. , 103 (1981) pp. 445–468
[a6]	C. Houzel, P. Schapira, "Images directes de modules différentiels" C.R. Acad. Paris Sér. I Math. , 298 (1984) pp. 461–464
[a7]	M. Kashiwara, "Systems of microdifferential equations" , Birkhäuser (1983) (Translated from French)
[a8]	M. Kashiwara, "The Riemann–Hilbert problem for holonomic systems" Publ. Res. Inst. Math. Sci. , 20 (1984) pp. 319–365
[a9]	M. Kashiwara, T. Kawai, "On the holonomic systems of micro-differential equations III" Publ. Res. Inst. Math. Sci. , 17 (1981) pp. 813–979
[a10]	D.T. Lê, Z. Mebkhout, "Introduction to linear differential systems" P. Orlik (ed.) , Singularities , Proc. Symp. Pure Math. , 40.2 , Amer. Math. Soc. (1983) pp. 31–63
[a11]	B. Malgrange, "Polynômes de Bernstein–Sato et cohomologie évanescente" Astérisque. Analyse et topologie sur les espaces singuliers (II-III) , 101–102 (1983) pp. 243–267
[a12]	Z. Mebkhout, "Théorèmes de bidualité locale pour les 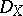-modules holonomes" Ark. Mat. , 20 (1982) pp. 111–124
[a13]	Z. Mebkhout, "Une autre équivalence de catégories" Compos. Math. , 51 (1984) pp. 63–88
[a14]	T. Oda, "Introduction to algebraic analysis on complex manifolds" S. Iitaka (ed.) , Algebraic varieties and analytic varieties , North-Holland (1983) pp. 29–48
[a15]	F. Pham, "Singularités des systèmes différentiels de Gauss–Manin" , Birkhäuser (1979)
[a16]	M. Saito, "Hodge structure via filtered -modules" Astérisque. Systèmes différentiels et singularités , 130 (1985) pp. 342–351
[a17]	M. Saito, "Modules de Hodge polarisables" Preprint RIMS , 553 (1986)
[a18]	P. Schapira, "Microdifferential systems in the complex domain" , Springer (1985)