Simplicial set
(formerly called semi-simplicial complex, full semi-simplicial complex)
A simplicial object in the category of sets 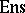 (cf. Simplicial object in a category), that is, a system of sets (
(cf. Simplicial object in a category), that is, a system of sets ( -fibres)
-fibres) 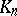 ,
,  , connected by mappings
, connected by mappings 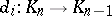 ,
,  (boundary operators), and
(boundary operators), and 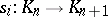 ,
, 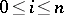 (degeneracy operators), satisfying the conditions
(degeneracy operators), satisfying the conditions
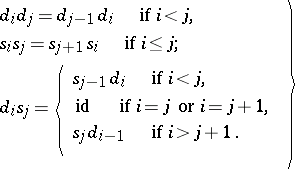 | (*) |
The elements of the fibre 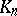 are called the
are called the  -dimensional simplices of the simplicial set
-dimensional simplices of the simplicial set 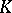 . If only the operators
. If only the operators 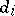 are given, satisfying the relations
are given, satisfying the relations 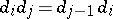 ,
, 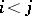 , then the system
, then the system 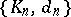 is called a semi-simplicial set.
is called a semi-simplicial set.
A simplicial mapping 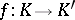 between two simplicial sets
between two simplicial sets 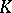 and
and 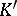 is a morphism of functors, i.e. a sequence of mappings
is a morphism of functors, i.e. a sequence of mappings 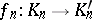 ,
, 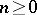 , satisfying the relations
, satisfying the relations
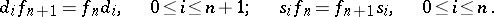 |
Simplicial sets and their simplicial mappings form a category, 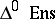 . If all the
. If all the  are imbeddings, then
are imbeddings, then 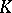 is called a simplicial subset of
is called a simplicial subset of  . In this case, the boundary and degeneracy operators in
. In this case, the boundary and degeneracy operators in 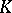 are the restrictions to
are the restrictions to 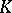 of the corresponding operators in
of the corresponding operators in 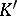 .
.
Given any topological space 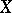 , one can define a simplicial set
, one can define a simplicial set 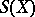 , called the singular simplicial set of the space
, called the singular simplicial set of the space 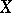 . Its simplices are the singular simplices of
. Its simplices are the singular simplices of 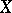 (see Singular homology), i.e. continuous mappings
(see Singular homology), i.e. continuous mappings 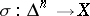 , where
, where  is the
is the  -dimensional geometric standard simplex:
-dimensional geometric standard simplex:
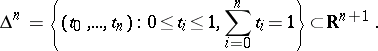 |
The boundary operators 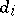 and degeneracy operators
and degeneracy operators 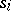 of this simplicial set are defined by the formulas
of this simplicial set are defined by the formulas
 |
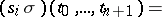 |
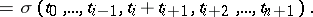 |
The correspondence 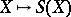 is a functor (called the singular functor) from the category of topological spaces
is a functor (called the singular functor) from the category of topological spaces  into the category of simplicial sets
into the category of simplicial sets 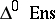 .
.
An arbitrary simplicial complex 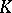 determines a simplicial set
determines a simplicial set 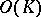 . Its
. Its  -dimensional simplices are the
-dimensional simplices are the  -tuples
-tuples 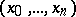 of vertices of
of vertices of 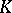 with the property that there is a simplex
with the property that there is a simplex  in
in 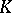 such that
such that 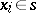 for
for 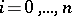 . The operators
. The operators 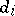 and
and 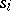 for this simplicial set are given by
for this simplicial set are given by
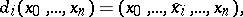 |
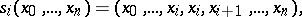 |
where  means that the symbol below it is omitted. If
means that the symbol below it is omitted. If 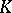 is ordered, then the simplices
is ordered, then the simplices 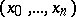 for which
for which 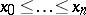 form a simplicial subset
form a simplicial subset  of
of 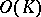 . The correspondence
. The correspondence 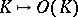 (
(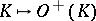 ) is a functor from the category of simplicial complexes (ordered simplicial complexes) into the category
) is a functor from the category of simplicial complexes (ordered simplicial complexes) into the category 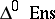 .
.
For an arbitrary group 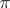 one can define a simplicial set
one can define a simplicial set 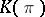 . Its
. Its  -simplices are equivalence classes of
-simplices are equivalence classes of 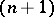 -tuples
-tuples 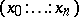 ,
, 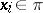 (where
(where 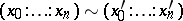 if there is an element
if there is an element 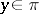 such that
such that 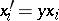 for all
for all 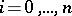 ). The operators
). The operators 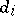 and
and 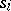 of
of 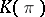 are given by
are given by
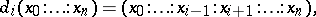 |
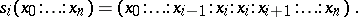 |
The simplicial set 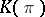 is actually a simplicial group.
is actually a simplicial group.
Given an arbitrary Abelian group 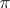 and any integer
and any integer 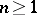 , one can define a simplicial set (in fact, a simplicial Abelian group)
, one can define a simplicial set (in fact, a simplicial Abelian group) 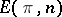 . Its
. Its 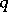 -dimensional simplices are the
-dimensional simplices are the  -dimensional cochains of the
-dimensional cochains of the 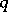 -dimensional geometric standard simplex
-dimensional geometric standard simplex 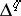 with coefficients in
with coefficients in 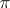 (that is,
(that is, 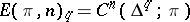 ). Denoting the vertices of
). Denoting the vertices of  by
by  ,
, 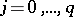 , one defines the simplicial mappings
, one defines the simplicial mappings 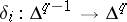 and
and  by the formulas
by the formulas
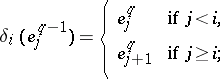 |
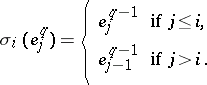 |
The induced homomorphisms of cochain groups
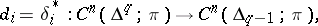 |
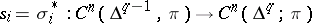 |
are, by definition, the boundary and degeneracy operators of the simplicial set 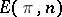 . The simplices that are cocycles form a simplicial subset of
. The simplices that are cocycles form a simplicial subset of 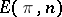 , called the Eilenberg–MacLane simplicial set and denoted by
, called the Eilenberg–MacLane simplicial set and denoted by 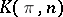 . The coboundary operator on the groups
. The coboundary operator on the groups 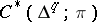 defines a canonical simplicial mapping
defines a canonical simplicial mapping 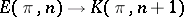 , denoted by
, denoted by 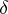 . Since the concept of a one-dimensional cocycle also makes sense when
. Since the concept of a one-dimensional cocycle also makes sense when  is non-Abelian (see Non-Abelian cohomology), the simplicial set
is non-Abelian (see Non-Abelian cohomology), the simplicial set 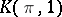 can be defined without the assumption that
can be defined without the assumption that 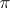 is Abelian. This simplicial set is isomorphic to the simplicial set
is Abelian. This simplicial set is isomorphic to the simplicial set 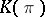 (by assigning to every simplex
(by assigning to every simplex 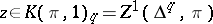 the values at the vertices
the values at the vertices 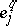 of a zero-dimensional cochain whose coboundary is
of a zero-dimensional cochain whose coboundary is  ).
).
By assigning to every fibre 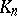 of a simplicial set
of a simplicial set 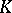 the free Abelian group generated by it, one obtains a simplicial Abelian group and thus a chain complex. This complex is denoted by
the free Abelian group generated by it, one obtains a simplicial Abelian group and thus a chain complex. This complex is denoted by 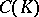 and is called the chain complex of
and is called the chain complex of 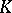 . The (co)homology groups of
. The (co)homology groups of 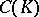 (with coefficients in a group
(with coefficients in a group 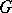 ) are called the (co) homology groups
) are called the (co) homology groups 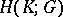 and
and 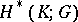 of
of 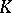 . The (co)homology groups of a singular simplicial set
. The (co)homology groups of a singular simplicial set 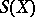 are the (co)homology groups of the space
are the (co)homology groups of the space 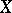 . The (co)homology groups of
. The (co)homology groups of 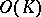 and
and 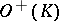 are isomorphic and are called the (co) homology groups of the simplicial complex
are isomorphic and are called the (co) homology groups of the simplicial complex 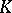 . The (co)homology groups of the simplicial set
. The (co)homology groups of the simplicial set  are the (co) homology groups of
are the (co) homology groups of 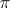 .
.
A simplex 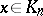 of a simplicial set
of a simplicial set 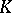 is called degenerate if there is a simplex
is called degenerate if there is a simplex  and a degeneracy operator
and a degeneracy operator 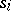 such that
such that 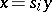 . The Eilenberg–Zil'ber lemma states that any simplex
. The Eilenberg–Zil'ber lemma states that any simplex  can be uniquely written in the form
can be uniquely written in the form 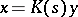 , where
, where  is a certain epimorphism
is a certain epimorphism 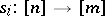 ,
, 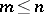 , and
, and 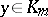 is a non-degenerate simplex. The smallest simplicial subset of a simplicial set
is a non-degenerate simplex. The smallest simplicial subset of a simplicial set 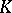 containing all its non-degenerate simplices of dimension at most
containing all its non-degenerate simplices of dimension at most  is denoted by
is denoted by 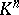 or
or  , and is called the
, and is called the  -dimensional skeleton or
-dimensional skeleton or  -skeleton of
-skeleton of 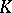 .
.
The standard geometric simplices (cf. Standard simplex)
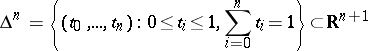 |
form a co-simplicial topological space with respect to the co-boundary operators  and co-degeneracy operators
and co-degeneracy operators 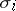 , defined by the formulas
, defined by the formulas
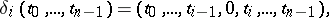 |
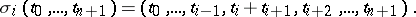 |
In the disjoint union 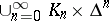 , where all the
, where all the 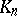 are regarded as discrete sets, the formulas
are regarded as discrete sets, the formulas
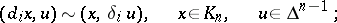 |
 |
generate an equivalence relation, the quotient space by which is a complex (a cellular space) whose cells are in one-to-one correspondence with the non-degenerate simplices of 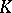 . This complex is denoted by
. This complex is denoted by 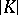 or
or 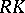 and is called the geometric realization in the sense of Milnor of
and is called the geometric realization in the sense of Milnor of 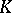 . Any simplicial mapping
. Any simplicial mapping 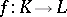 induces a continuous mapping
induces a continuous mapping 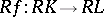 , given by
, given by
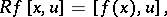 |
and the correspondence  ,
, 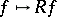 defines a functor
defines a functor 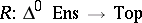 . This functor is left adjoint to the singular functor
. This functor is left adjoint to the singular functor 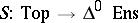 . The corresponding natural isomorphisms
. The corresponding natural isomorphisms
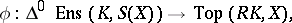 |
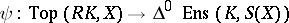 |
are defined by the formulas
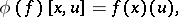 |
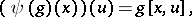 |
where
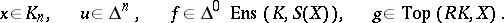 |
For any topological space 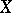 the adjunction morphism
the adjunction morphism 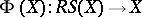 is a weak homotopy equivalence (which proves that any topological space is weakly homotopy equivalent to a complex).
is a weak homotopy equivalence (which proves that any topological space is weakly homotopy equivalent to a complex).
The construction of the geometric realization 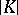 extends to the case of a simplicial topological space
extends to the case of a simplicial topological space 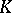 . One can also define the geometric realization
. One can also define the geometric realization 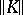 in the sense of Giever–Hu by taking only the boundary operators
in the sense of Giever–Hu by taking only the boundary operators  into account (in this model there are cells for all the simplices of
into account (in this model there are cells for all the simplices of 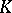 , not just for the non-degenerate ones). If every degeneracy operator
, not just for the non-degenerate ones). If every degeneracy operator 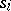 is a closed cofibration (a condition which holds automatically in the case of a simplicial set), then the natural mapping
is a closed cofibration (a condition which holds automatically in the case of a simplicial set), then the natural mapping 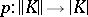 is a homotopy equivalence.
is a homotopy equivalence.
The category 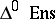 admits products: given simplicial sets
admits products: given simplicial sets  and
and 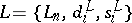 , their product is the simplicial set
, their product is the simplicial set 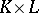 for which
for which
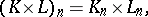 |
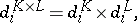 |
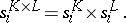 |
In particular, given any simplicial set 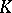 , one can define its product with the simplicial segment
, one can define its product with the simplicial segment 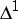 . The projections
. The projections 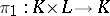 and
and 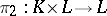 define a bijective mapping
define a bijective mapping
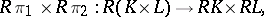 |
which is a homeomorphism if the product 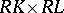 is a complex (for example, if both simplicial sets
is a complex (for example, if both simplicial sets 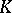 and
and 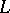 are countable or if one of the complexes
are countable or if one of the complexes 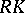 ,
, 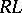 is locally finite). In particular, it follows that the geometric realization of any countable simplicial monoid (group, Abelian group) is a topological monoid (group, Abelian group).
is locally finite). In particular, it follows that the geometric realization of any countable simplicial monoid (group, Abelian group) is a topological monoid (group, Abelian group).
Two simplicial mappings 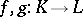 are called homotopic if there is a simplicial mapping (a homotopy)
are called homotopic if there is a simplicial mapping (a homotopy)  such that
such that
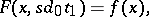 |
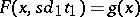 |
for any simplex  and for any composition
and for any composition  (of length
(of length  ) of degeneracy operators. This definition (modelled on the usual definition of homotopy of continuous mappings) is equivalent to the interpretation in simplicial sets of the general definition of homotopy of simplicial mappings between arbitrary simplicial objects (see Simplicial object in a category).
) of degeneracy operators. This definition (modelled on the usual definition of homotopy of continuous mappings) is equivalent to the interpretation in simplicial sets of the general definition of homotopy of simplicial mappings between arbitrary simplicial objects (see Simplicial object in a category).
Given the notion of homotopy, it is possible to develop a homotopy theory for simplicial sets similar to that for polyhedra. It turns out that these two theories are completely parallel; this finds expression in the fact that the corresponding homotopy categories are equivalent (the equivalence being induced by the geometric realization functor). In particular, geometric realizations of homotopic simplicial mappings are homotopic and, for example, the geometric realization of 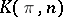 is the Eilenberg–MacLane space
is the Eilenberg–MacLane space 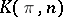 . However, the actual construction of the homotopy theory for simplicial sets differs slightly in its details from the construction of the homotopy theory for topological spaces. The main difference is that the relation of homotopy for simplicial mappings is not, in general, an equivalence relation. This difficulty is overcome in the following way.
. However, the actual construction of the homotopy theory for simplicial sets differs slightly in its details from the construction of the homotopy theory for topological spaces. The main difference is that the relation of homotopy for simplicial mappings is not, in general, an equivalence relation. This difficulty is overcome in the following way.
A simplicial mapping 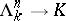 of the standard horn (see Standard simplex) into a simplicial set
of the standard horn (see Standard simplex) into a simplicial set 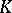 is called a horn in
is called a horn in 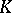 . Every horn is uniquely defined by an
. Every horn is uniquely defined by an 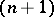 -tuple of
-tuple of  -simplices
-simplices 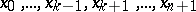 , for which
, for which  for all
for all 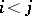 ,
,  . One says that a horn fills out if one can find an
. One says that a horn fills out if one can find an 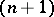 -dimensional simplex
-dimensional simplex  such that
such that 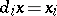 for every
for every 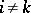 . The simplicial set
. The simplicial set 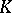 is said to be full (or to satisfy the Kan condition) if all its horns fill out.
is said to be full (or to satisfy the Kan condition) if all its horns fill out.
The singular simplicial set 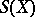 of an arbitrary topological space
of an arbitrary topological space 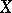 is always full, and so is every simplicial group; in particular, the Eilenberg–MacLane simplicial sets
is always full, and so is every simplicial group; in particular, the Eilenberg–MacLane simplicial sets 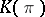 and
and  are full. The importance of full simplicial sets lies in the fact that the relation of homotopy between simplicial mappings from an arbitrary simplicial set to a full simplicial set is an equivalence relation. Therefore, in the subcategory of full simplicial sets, the construction of a homotopy theory involves no major difficulties. Moreover, there is a functor (see [4])
are full. The importance of full simplicial sets lies in the fact that the relation of homotopy between simplicial mappings from an arbitrary simplicial set to a full simplicial set is an equivalence relation. Therefore, in the subcategory of full simplicial sets, the construction of a homotopy theory involves no major difficulties. Moreover, there is a functor (see [4]) 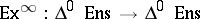 assigning to every simplicial set
assigning to every simplicial set 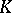 a full simplicial set,
a full simplicial set, 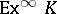 , whose geometric realization is homotopy equivalent to the geometric realization of
, whose geometric realization is homotopy equivalent to the geometric realization of 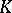 and which can therefore be used in place of
and which can therefore be used in place of 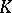 in all questions of homotopy.
in all questions of homotopy.
Two  -simplices
-simplices  and
and 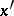 of a simplicial set
of a simplicial set 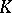 are called comparable if
are called comparable if 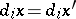 ,
, 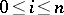 . Two such simplices are said to be homotopic if there is an
. Two such simplices are said to be homotopic if there is an 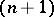 -dimensional simplex
-dimensional simplex  such that
such that 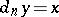 ,
, 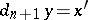 and
and 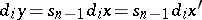 ,
, 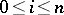 . For full simplicial sets this is an equivalence relation, and two simplices are homotopic if and only if their characteristic simplicial mappings are homotopic
. For full simplicial sets this is an equivalence relation, and two simplices are homotopic if and only if their characteristic simplicial mappings are homotopic 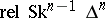 .
.
A simplicial set 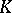 is said to be pointed if it contains a distinguished zero-dimensional simplex
is said to be pointed if it contains a distinguished zero-dimensional simplex  (where the symbol
(where the symbol 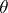 is also used to denote all degenerations of this simplex as well as the simplicial set generated by it, which is usually referred to as the distinguished point of
is also used to denote all degenerations of this simplex as well as the simplicial set generated by it, which is usually referred to as the distinguished point of  ). For a full pointed simplicial set
). For a full pointed simplicial set 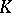 , the set
, the set 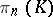 of homotopy classes of
of homotopy classes of  -dimensional simplices comparable with
-dimensional simplices comparable with 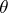 is a group when
is a group when 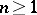 . This group is called the
. This group is called the  -dimensional homotopy group of
-dimensional homotopy group of 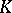 ; this terminology is justified by the fact that
; this terminology is justified by the fact that 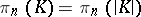 and, in particular,
and, in particular, 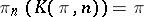 and
and 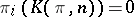 for
for 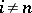 . A simplicial set
. A simplicial set 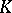 for which
for which 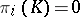 for all
for all  is called an
is called an  -connected set; in particular, a
-connected set; in particular, a  -connected simplicial set is called connected, and a
-connected simplicial set is called connected, and a 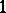 -connected simplicial set simply connected. For
-connected simplicial set simply connected. For 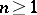 , the addition in
, the addition in 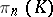 is induced by the operation which assigns to two simplices
is induced by the operation which assigns to two simplices  and
and 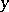 (comparable with
(comparable with  ) the simplex
) the simplex 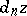 , where
, where  is a simplex of dimension
is a simplex of dimension 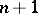 , filling the horn
, filling the horn 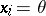 ,
, 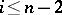 ,
, 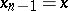 ,
, 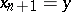 . If
. If 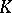 is a simplicial monoid with unit
is a simplicial monoid with unit 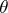 , then the addition is also induced by the multiplication in this monoid (the product of two simplices comparable with
, then the addition is also induced by the multiplication in this monoid (the product of two simplices comparable with 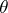 is comparable with
is comparable with  ).
).
Since any simplex  comparable with
comparable with 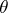 is a cycle (of the chain complex
is a cycle (of the chain complex 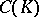 defined by
defined by 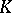 ), there is a natural Hurewicz homomorphism
), there is a natural Hurewicz homomorphism 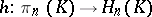 , which induces an isomorphism
, which induces an isomorphism
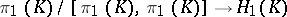 |
when  (Poincaré's theorem), and for
(Poincaré's theorem), and for 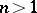 it is an isomorphism if
it is an isomorphism if  is
is 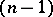 -connected (Hurewicz' theorem). For full simplicial sets both variants of Whitehead's theorem hold, that is, a simplicial mapping
-connected (Hurewicz' theorem). For full simplicial sets both variants of Whitehead's theorem hold, that is, a simplicial mapping 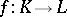 of full simplicial sets is a homotopy equivalence if and only if it induces an isomorphism of homotopy groups; in the simply-connected case this condition is equivalent to the induced homomorphisms of the homology groups being isomorphisms.
of full simplicial sets is a homotopy equivalence if and only if it induces an isomorphism of homotopy groups; in the simply-connected case this condition is equivalent to the induced homomorphisms of the homology groups being isomorphisms.
In the case when 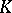 is a simplicial group, the homotopy group
is a simplicial group, the homotopy group 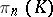 is isomorphic to the homology group
is isomorphic to the homology group 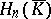 of the (not necessarily Abelian) chain complex
of the (not necessarily Abelian) chain complex 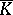 for which
for which
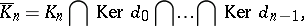 |
and the boundary operator is the restriction to 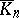 of
of  . If
. If 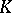 is Abelian, then
is Abelian, then 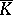 is a subcomplex of
is a subcomplex of 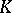 , regarded as a chain complex, and also a chain deformation retract of it, and hence a direct summand of it. It turns out that the subcomplex generated by the degenerate simplices can be taken as the other direct summand. Therefore, the corresponding quotient complex of
, regarded as a chain complex, and also a chain deformation retract of it, and hence a direct summand of it. It turns out that the subcomplex generated by the degenerate simplices can be taken as the other direct summand. Therefore, the corresponding quotient complex of 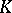 is chainwise equivalent to it. For example, it follows that the cohomology groups of an arbitrary simplicial set
is chainwise equivalent to it. For example, it follows that the cohomology groups of an arbitrary simplicial set 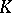 are isomorphic to the normalized cohomology groups (the normalization theorem), that is, the groups obtained from the cochains that vanish on all degenerate simplices. Furthermore,
are isomorphic to the normalized cohomology groups (the normalization theorem), that is, the groups obtained from the cochains that vanish on all degenerate simplices. Furthermore, 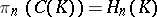 .
.
The functor 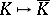 induces an equivalence between the homotopy theory of simplicial Abelian groups and the homology theory of chain complexes. In particular, it follows that any connected simplicial Abelian group
induces an equivalence between the homotopy theory of simplicial Abelian groups and the homology theory of chain complexes. In particular, it follows that any connected simplicial Abelian group 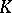 is homotopy equivalent to a product of Eilenberg–MacLane simplicial sets
is homotopy equivalent to a product of Eilenberg–MacLane simplicial sets 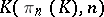 .
.
A full simplicial set 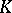 is called minimal when comparable simplices are homotopic if and only if they coincide. The simplicial set
is called minimal when comparable simplices are homotopic if and only if they coincide. The simplicial set 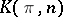 is minimal. Every homotopy equivalence of minimal simplicial sets is an isomorphism. Every full simplicial set
is minimal. Every homotopy equivalence of minimal simplicial sets is an isomorphism. Every full simplicial set 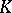 has a minimal subset. It is a deformation retract, and is thus uniquely defined up to isomorphism.
has a minimal subset. It is a deformation retract, and is thus uniquely defined up to isomorphism.
A simplicial mapping 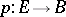 is called a Kan fibration if any horn
is called a Kan fibration if any horn 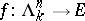 in
in 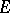 can be filled whenever
can be filled whenever 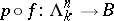 can be, and for any filling
can be, and for any filling 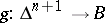 of
of 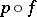 there is a filling
there is a filling 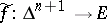 of
of  such that
such that 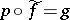 . Kan fibrations are the simplicial analogue of Serre fibrations (cf. Serre fibration), and they satisfy the following homotopy lifting theorem: If the simplicial mappings
. Kan fibrations are the simplicial analogue of Serre fibrations (cf. Serre fibration), and they satisfy the following homotopy lifting theorem: If the simplicial mappings  and
and 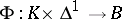 satisfy the equation
satisfy the equation 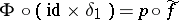 , then there is a simplicial mapping
, then there is a simplicial mapping 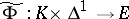 such that
such that 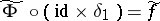 and
and 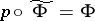 . If the fibration
. If the fibration 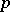 is surjective, then
is surjective, then 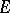 is full if and only if
is full if and only if 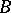 is full. The fibre of
is full. The fibre of 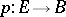 is the (automatically full) simplicial set
is the (automatically full) simplicial set 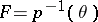 , where
, where 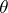 is the distinguished point of
is the distinguished point of 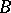 . For any Serre fibration
. For any Serre fibration 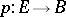 the simplicial mapping
the simplicial mapping 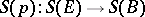 is a Kan fibration, and for any Kan fibration
is a Kan fibration, and for any Kan fibration  the mapping
the mapping 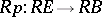 is a Serre fibration (see [5]).
is a Serre fibration (see [5]).
Let 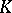 be a full pointed simplicial set and let
be a full pointed simplicial set and let 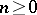 . Write
. Write 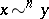 for
for 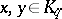 when
when 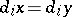 for all
for all 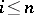 , that is, when
, that is, when
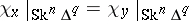 |
(see Standard simplex). This is an equivalence relation, and the quotient sets 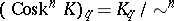 form a simplicial set
form a simplicial set 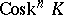 (with respect to the induced boundary and degeneracy operators), called the
(with respect to the induced boundary and degeneracy operators), called the  -co-skeleton of
-co-skeleton of 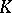 . By definition,
. By definition, 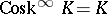 . For any
. For any 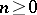 , the simplicial set
, the simplicial set 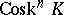 is full and
is full and 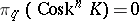 when
when 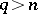 . Moreover, for any
. Moreover, for any 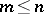 the natural surjective simplicial mapping
the natural surjective simplicial mapping
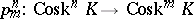 |
is a fibration inducing an isomorphism of homotopy groups in dimensions less than or equal to 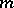 . In particular, the fibre of
. In particular, the fibre of 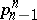 is homotopy equivalent to the Eilenberg–MacLane simplicial set
is homotopy equivalent to the Eilenberg–MacLane simplicial set  . The sequence of fibrations
. The sequence of fibrations
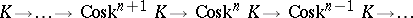 |
is called the Postnikov system of a full simplicial set 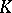 . If
. If 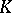 is minimal, then this sequence is a resolution of
is minimal, then this sequence is a resolution of 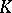 (see Homotopy type).
(see Homotopy type).
The construction of the Postnikov system admits a direct generalization to an arbitrary fibration 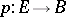 of a full simplicial set
of a full simplicial set 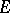 over a full simplicial set
over a full simplicial set 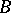 . Let
. Let 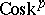 be the simplicial set whose fibres
be the simplicial set whose fibres 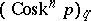 are the quotient sets of the fibres
are the quotient sets of the fibres 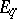 by the relation
by the relation  , which holds if and only if
, which holds if and only if 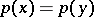 and
and 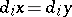 for all
for all 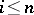 . By definition,
. By definition, 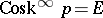 . Note that
. Note that 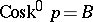 . For
. For 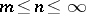 the natural simplicial mapping
the natural simplicial mapping
 |
is a fibration inducing an isomorphism of homotopy groups in dimensions less than or equal to 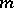 or greater than
or greater than 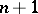 . In particular, the fibre of
. In particular, the fibre of 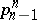 is homotopy equivalent to the Eilenberg–MacLane simplicial set
is homotopy equivalent to the Eilenberg–MacLane simplicial set 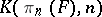 . The fibre of
. The fibre of 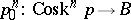 is the simplicial set
is the simplicial set 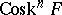 , where
, where 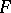 is the fibre of
is the fibre of 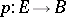 . The sequence of fibrations
. The sequence of fibrations
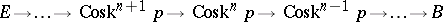 |
is called the Moore–Postnikov system of 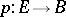 .
.
It is convenient to define spectra in the language of simplicial sets. A simplicial spectrum is a sequence 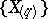 of pointed sets (whose elements are called simplices, and the distinguished simplex is denoted by
of pointed sets (whose elements are called simplices, and the distinguished simplex is denoted by 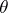 ) defined for any integer
) defined for any integer 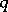 , and equipped with mappings
, and equipped with mappings 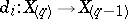 ,
, 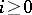 (boundary operators), and
(boundary operators), and  ,
, 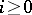 (degeneracy operators), which satisfy the relations (*) together with the following condition: For every simplex
(degeneracy operators), which satisfy the relations (*) together with the following condition: For every simplex 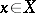 there is an integer
there is an integer  such that
such that 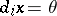 when
when 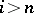 . To any spectrum
. To any spectrum 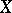 and integer
and integer  one can assign the simplicial set
one can assign the simplicial set 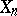 defined by
defined by
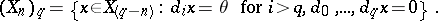 |
These simplicial sets 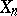 are equipped with imbeddings
are equipped with imbeddings 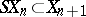 , where
, where 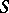 is the suspension functor. From the sequence of simplicial sets
is the suspension functor. From the sequence of simplicial sets 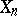 and imbeddings
and imbeddings 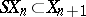 , the simplicial spectrum
, the simplicial spectrum 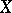 can in turn be uniquely recovered. If every member of
can in turn be uniquely recovered. If every member of 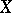 is full, then
is full, then 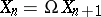 , where
, where  is the loop functor. The geometric realization functor gives an equivalence of the category of simplicial spectra and the category of topological spectra. Simplicial spectra can be defined for an arbitrary category. The category of Abelian group spectra is isomorphic to the category of (Abelian) chain complexes.
is the loop functor. The geometric realization functor gives an equivalence of the category of simplicial spectra and the category of topological spectra. Simplicial spectra can be defined for an arbitrary category. The category of Abelian group spectra is isomorphic to the category of (Abelian) chain complexes.
References
| [1] | P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967) |
| [2] | J.P. May, "Simplicial objects in algebraic topology" , v. Nostrand (1967) |
| [3] | K. Lamotke, "Semisimpliziale algebraische Topologie" , Springer (1968) |
| [4] | D.M. Kan, "On c.s.s. complexes" Amer. J. Math. , 79 (1957) pp. 449–476 |
| [5] | D.G. Quillen, "The geometric realization of a Kan fibration is a Serre fibration" Proc. Amer. Math. Soc. , 19 (1968) pp. 1499–1500 |
| [6] | E.H. Brown, "Finite computability of Postnikov complexes" Ann. of Math. (2) , 65 (1957) pp. 1–20 |
| [7] | D.M. Kan, "A combinatorial definition of homotopy groups" Ann. of Math. (2) , 67 (1958) pp. 282–312 |
| [8] | D.M. Kan, "On homotopy theory and c.s.s. groups" Ann. of Math. (2) , 68 (1958) pp. 38–53 |
| [9] | D.M. Kan, "An axiomatization of the homotopy groups" Illinois J. Math. , 2 (1958) pp. 548–566 |
| [10] | D.M. Kan, "A relation between CW-complexes and free c.s.s. groups" Amer. J. Math. , 81 (1959) pp. 512–528 |
Comments
The "Kan condition" that every horn fills out is also called the extension condition.
A simplicial set or simplicial complex 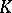 is called a Kan complex if it satisfies the Kan condition, [2], p. 2.
is called a Kan complex if it satisfies the Kan condition, [2], p. 2.
Let 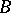 be the set of all monomorphisms
be the set of all monomorphisms 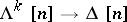 of horns.
of horns.
A class of monomorphisms 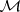 in a category is called saturated if it satisfies the following conditions:
in a category is called saturated if it satisfies the following conditions:
i) all isomorphisms belong to 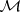 ;
;
ii) let
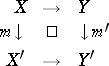 |
be a co-Cartesian square. Then if 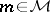 , also
, also 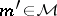 (stability of
(stability of 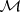 under pushouts; a co-Cartesian square is a Cartesian square in the dual category);
under pushouts; a co-Cartesian square is a Cartesian square in the dual category);
iii) given a commutative diagram
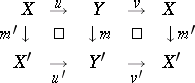 |
with 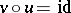 ,
, 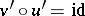 and
and 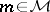 , then
, then 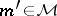 (stability of
(stability of 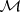 under retractions);
under retractions);
iv) 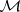 is stable under countable compositions and arbitrary direct sums.
is stable under countable compositions and arbitrary direct sums.
Let 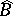 be the saturated closure of
be the saturated closure of 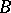 , i.e. the intersection of all saturated classes containing
, i.e. the intersection of all saturated classes containing 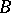 . These are called the anodyne extensions in [1].
. These are called the anodyne extensions in [1].
A morphism 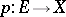 of
of 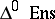 is called a Kan fibration if for each anodyne extension
is called a Kan fibration if for each anodyne extension 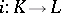 and commutative square
and commutative square
 |
there exists a morphism 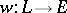 such that
such that 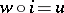 and
and 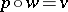 . A simplicial set
. A simplicial set 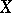 is a Kan complex if and only if the unique morphism
is a Kan complex if and only if the unique morphism 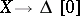 , where
, where 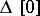 is the standard zero simplex, is a Kan fibration.
is the standard zero simplex, is a Kan fibration.
Simplicial set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simplicial_set&oldid=16248