Finitely-determined function

A lexical function characterizing the behaviour of a finite automaton (cf. Automaton, finite). (A function is called lexical if its domain of definition and range of values are sets of words or superwords.)

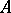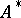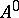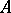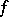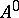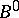Suppose that is an alphabet. Let denote the set of all words, and the set of all words or the set of all superwords over . A function mapping into , where 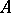and 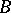are any finite alphabets, is called a determined function if it satisfies the following two conditions:

1) for any 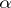in 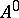, the length of 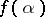is equal to the length of 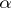; and

2) if 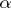is a word of length 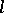and 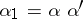, , 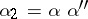where 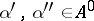, then the values and 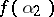have the same beginnings of length .

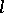If a determined function 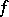is defined on the set 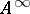of all superwords over 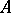then, by conditions 1) and 2), it can be extended to the set 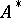: For an arbitrary word of length 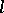, the value 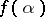coincides with the beginning of length 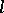of the value 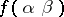, where 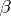is an arbitrary superword over 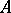. Thus, every determined function 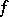satisfies the condition:

3) for any word 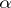in 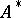and any in 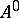one has , where 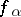is a determined function on the set , uniquely determined by the word .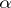

The function 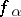is called the remainder function for 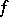. Condition 3) implies that every determined function defines an equivalence relation 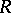on the set 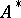: 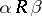if and only if 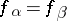. The rank of this relation, or, which comes to the same thing, the maximum number of pairwise-distinct remainder functions, is called the weight of the determined function 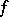. If the weight of a determined function is finite, then the function is called a finitely-determined function. This concept can also be extended to functions of 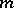variables, where 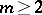, if a collection of 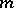words of the same length (or superwords) over alphabets 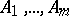, respectively, is considered as a word (superword) over the alphabet 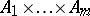— the Cartesian product of 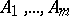. Thus, one can consider finitely-determined functions with several outcomes, that is, whose values are sets of words or superwords over alphabets , respectively. The class of all finitely-determined functions coincides with the class of functions computable by finite automata. Hence the same means may be used to represent finitely-determined functions as are used to represent finite automata, e.g. canonical equations (see Automaton, finite; Automata, methods of specification of). This implies, in particular, that the class of finitely-determined functions with coincident alphabets 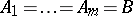is closed under superposition. The minimal (in number of states) automaton 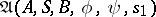computing a finitely-determined function of weight contains states and can be constructed as follows. Let be arbitrary representatives of the equivalence classes under the relation 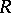. To each class 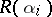, , 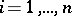corresponds a state 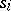of the automaton 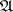. The transition function 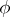and the output function 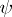are defined by the following conditions: If 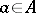and 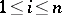, then 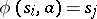, the state 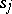corresponds to the class 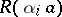; 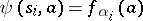. The initial state is taken as that corresponding to the class 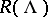, where 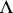is the empty word.

References

[1]	S.C. Kleene, "Representation of events in nerve nets and finite automata" , Automata studies , 34 , Princeton Univ. Press (1956) pp. 3–41
[2]	S.V. Yablonskii, "Introduction to discrete mathematics" , Moscow (1986) (In Russian)

Comments

(Finitely-) determined functions are also called (finite) sequential machine mappings or Mealy mappings. They are a special case of gsm-mappings, for which condition 1) above is not required.

Instead of "remainder function" one also uses derivative.

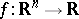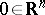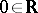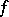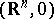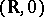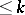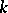A rather different notion of finite determinacy of functions occurs in differential topology. Let be a smooth function taking to . Roughly, a function is finitely determined at if up to local diffeomorphisms of and it is uniquely determined near 0 by the terms of order of its Taylor series at ; it is then said to be -determined. The precise notions involve germs (cf. Germ) of functions and mappings. Cf. Singularities of differentiable mappings for more details (in a more general setting) and for related notions such as stable germs of differentiable mappings, singularities of finite type, etc.

References

[a1]	S. Ginsburg, "The mathematical theory of context-free languages" , McGraw-Hill (1965)
[a2]	J.E. Hopcroft, J.D. Ulman, "Introduction to automata theory, languages and computation" , Addison-Wesley (1979)