Banach function space
Let 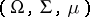 be a complete
be a complete 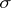 -finite measure space and let
-finite measure space and let 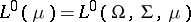 be the space of all equivalence classes of
be the space of all equivalence classes of 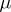 -measurable real-valued functions endowed with the topology of convergence in measure relative to each set of finite measure.
-measurable real-valued functions endowed with the topology of convergence in measure relative to each set of finite measure.
A Banach space 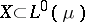 is called a Banach function space on
is called a Banach function space on 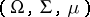 if there exists a
if there exists a 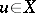 such that
such that 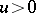 almost everywhere and
almost everywhere and 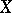 satisfies the ideal property:
satisfies the ideal property:
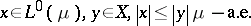 |
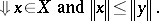 |
The Lebesgue function spaces 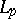 (
(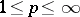 ) play a primary role in many problems arising in mathematical analysis. There are other classes of Banach function spaces that are also of interest. The classes of Musielak–Orlicz, Lorentz and Marcinkiewicz spaces, for example, are of intrinsic importance (cf. also Orlicz space; Orlicz–Lorentz space; Marcinkiewicz space). Function spaces are important and natural examples of abstract Banach lattices (a Banach lattice is a Banach space that is also a vector lattice
) play a primary role in many problems arising in mathematical analysis. There are other classes of Banach function spaces that are also of interest. The classes of Musielak–Orlicz, Lorentz and Marcinkiewicz spaces, for example, are of intrinsic importance (cf. also Orlicz space; Orlicz–Lorentz space; Marcinkiewicz space). Function spaces are important and natural examples of abstract Banach lattices (a Banach lattice is a Banach space that is also a vector lattice 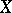 with the property that
with the property that 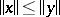 whenever
whenever 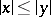 , where
, where 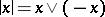 , cf. also Banach lattice). A Banach lattice is said to be order continuous if
, cf. also Banach lattice). A Banach lattice is said to be order continuous if 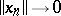 whenever
whenever 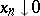 . The following very useful general representation result (see [a12]) allows one to reduce most of the proofs for a quite large class of abstract Banach lattices to the case of Banach function spaces: Let
. The following very useful general representation result (see [a12]) allows one to reduce most of the proofs for a quite large class of abstract Banach lattices to the case of Banach function spaces: Let 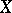 be an order-continuous Banach lattice with a weak unit (a weak unit is an element
be an order-continuous Banach lattice with a weak unit (a weak unit is an element 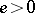 such that
such that 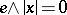 implies
implies 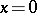 ). Then there exist a probability space
). Then there exist a probability space 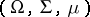 and a Banach function space
and a Banach function space 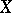 on
on 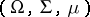 such that
such that 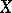 is isometrically lattice-isomorphic to
is isometrically lattice-isomorphic to 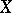 and
and 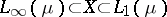 with continuous inclusions.
with continuous inclusions.
See [a2], [a7], [a10], [a14] for a general theory of Banach lattices.
A Banach function space 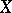 is said to have the Fatou property if whenever
is said to have the Fatou property if whenever 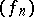 is a norm-bounded sequence in
is a norm-bounded sequence in 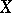 such that
such that 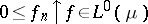 , then
, then  and
and 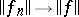 .
.
In recent (1998) years a great deal of research went into the study of rearrangement-invariant function spaces, in particular of Orlicz spaces. General references to this area are e.g. [a7], [a11], [a12]. A Banach function space 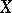 is said to be rearrangement invariant if whenever
is said to be rearrangement invariant if whenever 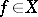 ,
, 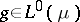 , and
, and 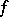 and
and 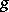 are equi-measurable, then
are equi-measurable, then 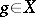 and
and 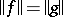 . Two functions
. Two functions 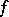 and
and 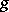 are called equi-measurable if
are called equi-measurable if 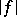 and
and 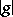 have identical distributions, that is,
have identical distributions, that is,
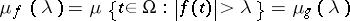 |
for all 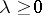 .
.
In the study of rearrangement-invariant function spaces, the Boyd indices play an important role (see e.g. [a7], [a12], and Boyd index). The Boyd indices  and
and 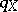 of a rearrangement-invariant function space
of a rearrangement-invariant function space 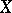 on
on 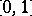 or
or 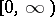 are defined by
are defined by
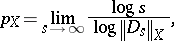 |
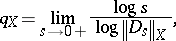 |
where for 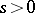 ,
, 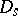 denotes the dilation operator, defined by
denotes the dilation operator, defined by  for
for 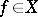 (where
(where  is defined to be zero outside
is defined to be zero outside 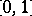 in the former case).
in the former case).
For example, consider the following results, which hold for every separable rearrangement-invariant function space  on
on 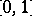 :
:
i) 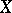 has an unconditional basis if and only if
has an unconditional basis if and only if 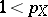 and
and 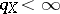 (see, e.g., [a11], [a12]);
(see, e.g., [a11], [a12]);
ii) if 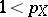 and
and 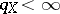 , then
, then 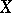 is a primary, i.e., whenever
is a primary, i.e., whenever  , then at least one of
, then at least one of 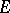 and
and 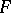 is isomorphic to
is isomorphic to 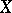 (see [a3]).
(see [a3]).
Rearrangement-invariant function spaces play an important role in the theory of interpolation of operators (see [a4], [a11]). A remarkable result of A.P. Calderón [a5] on the characterization of all interpolation spaces between 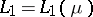 and
and 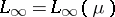 asserts that
asserts that 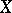 is an interpolation space with respect to the couple
is an interpolation space with respect to the couple 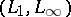 (i.e., that every linear operator
(i.e., that every linear operator 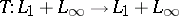 such that
such that 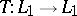 and
and 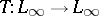 boundedly, also maps
boundedly, also maps 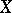 to
to 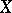 boundedly) if and only if it has the following property: For every
boundedly) if and only if it has the following property: For every 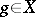 and every
and every 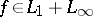 , whenever
, whenever 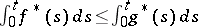 for all
for all 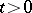 , it follows that
, it follows that 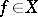 and
and 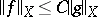 for some absolute constant
for some absolute constant 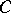 .
.
Here, 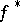 denotes the non-increasing rearrangement of
denotes the non-increasing rearrangement of 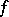 , which is defined by
, which is defined by
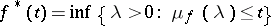 |
for 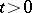 . In particular, Calderón's result implies that rearrangement-invariant function spaces which have the Fatou property or are separable are interpolation spaces between
. In particular, Calderón's result implies that rearrangement-invariant function spaces which have the Fatou property or are separable are interpolation spaces between 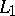 and
and 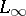 .
.
The Köthe dual space 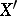 of a Banach function space
of a Banach function space 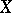 on
on 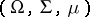 is defined to be the space of all
is defined to be the space of all 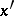 for which
for which 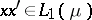 for each
for each 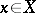 (cf. also Köthe–Toeplitz dual). The space
(cf. also Köthe–Toeplitz dual). The space 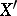 is a Banach function space endowed with the norm
is a Banach function space endowed with the norm
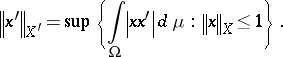 |
Moreover, 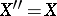 isometrically if and only if
isometrically if and only if 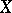 has the Fatou property.
has the Fatou property.
It is important to describe the relation between the Köthe dual 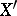 and the usual (topological) dual space
and the usual (topological) dual space 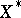 of a Banach function space
of a Banach function space 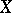 . A linear functional
. A linear functional  on
on 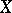 is said to be order continuous (or integral) if
is said to be order continuous (or integral) if 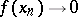 for every sequence
for every sequence 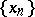 in
in 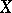 such that
such that 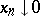 almost everywhere. Let
almost everywhere. Let 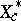 be the space all order-continuous functionals. This is a closed and norm-one complemented subspace of
be the space all order-continuous functionals. This is a closed and norm-one complemented subspace of 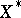 . Thus,
. Thus, 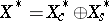 , where
, where 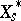 denotes a complement to
denotes a complement to 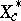 , called the space of all singular functionals on
, called the space of all singular functionals on 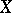 . The space
. The space 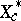 is always total on
is always total on  (cf. Total set). Furthermore, it is norming, i.e.,
(cf. Total set). Furthermore, it is norming, i.e.,
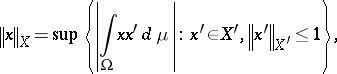 |
if and only if the norm on 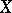 is order semi-continuous, i.e.,
is order semi-continuous, i.e., 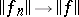 whenever
whenever 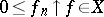 . The mapping that assigns to every
. The mapping that assigns to every 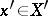 the functional
the functional 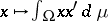 on
on  is an order-linear isometry from the Köthe dual space
is an order-linear isometry from the Köthe dual space 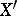 onto
onto 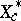 . In this way
. In this way 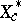 is identified with
is identified with 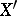 . In particular, if
. In particular, if 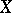 is an order-continuous Banach function space, then
is an order-continuous Banach function space, then 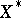 can be identified with
can be identified with  (see [a10], [a12], [a14]).
(see [a10], [a12], [a14]).
There are many methods of constructing Banach function spaces which are intermediate in some sense between two given Banach function spaces. One such method is the following construction, again due to Calderón [a5]. See also [a13] for the generalized version due to G.A. Lozanovskii. Let 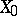 and
and 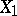 be two Banach function spaces on the same measure space
be two Banach function spaces on the same measure space 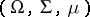 . For each
. For each 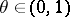 , the lattice
, the lattice 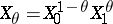 is defined to be the space of all
is defined to be the space of all 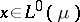 such that
such that 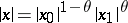
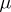 -almost everywhere for some
-almost everywhere for some  and
and 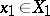 . The space
. The space 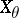 is a Banach function space endowed with the norm
is a Banach function space endowed with the norm
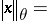 |
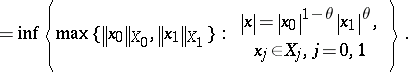 |
The identity 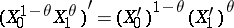 for all
for all 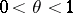 is an important result proved by Lozanovskii [a13]. Closely related results are the formula
is an important result proved by Lozanovskii [a13]. Closely related results are the formula 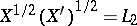 , which holds for any Banach function space on
, which holds for any Banach function space on  , and also the Lozanovskii factorization theorem: For every
, and also the Lozanovskii factorization theorem: For every 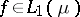 and
and 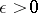 there exist
there exist 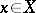 and
and 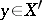 such that
such that 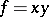 and
and 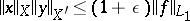 . If
. If 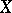 has the Fatou property, the theorem is true for
has the Fatou property, the theorem is true for 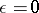 as well.
as well.
This theorem has proved to be very useful in various applications (see, for example, [a9], [a15]).
Calderón's construction has found many other interesting applications in the study of Banach function spaces. An example is Pisier's theorem [a16], which says that if 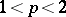 , then a Banach function space on
, then a Banach function space on 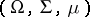 is
is 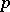 -convex and
-convex and 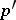 -concave if and only if
-concave if and only if 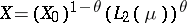 for some Banach function space
for some Banach function space 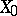 on
on 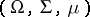 , with
, with 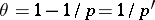 . An application of this result and interpolation yields the following (see [a16]): Let
. An application of this result and interpolation yields the following (see [a16]): Let 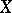 be a
be a 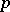 -convex and
-convex and 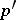 -concave Banach function space for some
-concave Banach function space for some 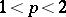 . Then every bounded linear operator from an
. Then every bounded linear operator from an 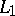 -space into
-space into  is
is 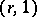 -summing with
-summing with 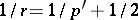 , i.e., if
, i.e., if 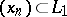 is such that
is such that 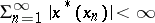 for all
for all 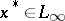 , then
, then 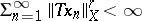 (cf. also Absolutely summing operator).
(cf. also Absolutely summing operator).
For another example see [a6], where the Calderón construction is used to construct a class of super-reflexive and complementably minimal Banach spaces (i.e., such that every infinite-dimensional closed subspace contains a complemented subspace isomorphic to a given space of this class) which are not isomorphic to 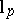 for any
for any 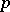 .
.
One of the most interesting problems in the theory of Banach function spaces is to determine when two Banach function spaces which are isomorphic as Banach spaces are also lattice isomorphic. The first result of this type, due to Y.A. Abramovich and P. Wojtaszczyk [a1] says that 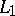 has a unique structure as a non-atomic Banach function space (i.e., if
has a unique structure as a non-atomic Banach function space (i.e., if 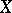 is a non-atomic Banach function space isomorphic to
is a non-atomic Banach function space isomorphic to 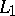 , then
, then 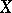 is lattice isomorphic to
is lattice isomorphic to  ). The general study of possible rearrangement-invariant lattice structures in in Banach function spaces on
). The general study of possible rearrangement-invariant lattice structures in in Banach function spaces on 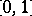 or
or 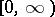 was initiated in [a7], where, among other important results, it is shown that any rearrangement-invariant function space
was initiated in [a7], where, among other important results, it is shown that any rearrangement-invariant function space 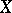 on
on 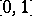 which is isomorphic to
which is isomorphic to 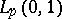 ,
,  , is equal to
, is equal to 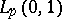 up to an equivalent renorming. See also [a8], where important general results on the uniqueness of the structure of Banach function spaces are presented.
up to an equivalent renorming. See also [a8], where important general results on the uniqueness of the structure of Banach function spaces are presented.
References
| [a1] | Y.A. Abramovich, P. Wojtaszczyk, "On the uniqueness of order in the spaces 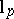 and and 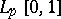 " Mat. Zametki , 18 (1975) pp. 313–325 " Mat. Zametki , 18 (1975) pp. 313–325 |
| [a2] | C.D. Aliprantis, O. Burkinshaw, "Positive operators" , Acad. Press (1995) |
| [a3] | D. Alspach, P. Enflo, E. Odell, "On the structure of separable 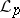 spaces, spaces, 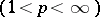 " Studia Math. , 60 (1977) pp. 79–90 " Studia Math. , 60 (1977) pp. 79–90 |
| [a4] | C. Bennett, R. Sharpley, "Interpolation of operators" , Acad. Press (1988) |
| [a5] | A.P. Calderón, "Intermediate spaces and interpolation, the complex method" Studia Math. , 24 (1964) pp. 113–190 |
| [a6] | P.G. Casazza, N.J. Kalton, D. Kutzarova, M. Mastylo, "Complex interpolation and complementably minimal spaces" N. Kalton (ed.) E. Saab (ed.) S. Montgomery-Smith (ed.) , Interaction between Functional Analysis, Harmonic Analysis, and Probability (Proc. Conf. Univ. Missouri 1994) , Lecture Notes Pure Appl. Math. , 175 , M. Dekker (1996) pp. 135–143 |
| [a7] | W.B. Johnson, B. Maurey, V. Schechtmannn, L. Tzafriri, "Symmetric structures in Banach spaces" Memoirs Amer. Math. Soc. , 217 (1979) |
| [a8] | N.J. Kalton, "Lattice structures on Banach spaces" Memoirs Amer. Math. Soc. , 493 (1993) |
| [a9] | N.J. Kalton, "The basic sequence problem" Studia Math. , 116 (1995) pp. 167–187 |
| [a10] | L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1998) |
| [a11] | S.G. Krein, Yu.I. Petunin, E.M. Semenov, "Interpolation of linear operators" , Amer. Math. Soc. (1982) (In Russian) |
| [a12] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces: Function spaces" , 2 , Springer (1979) |
| [a13] | G.A. Lozanovskii, "On some Banach lattices" Sib. Math. J. , 10 (1969) pp. 419–430 |
| [a14] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , 2 , North-Holland (1983) |
| [a15] | E. Odell, T. Schlumprecht, "The distortion problem" Acta Math. , 173 (1994) pp. 258–281 |
| [a16] | G. Pisier, "Some applications of the complex interpolation method to Banach lattices" J. Anal. Math. , 35 (1979) pp. 264–281 |
Banach function space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_function_space&oldid=16221