Partition

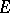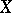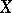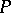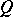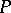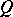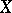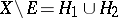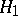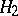A closed set in a topological space that partitions between two given sets and (or, in other words, separates and in ), i.e. such that , where and are disjoint and open in 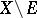, , 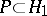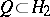( 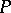and 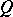are open in all of 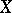). A partition is called fine if its interior is empty. Any binary decomposition (i.e. a partition consisting of two elements) 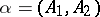of a space 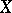defines a fine partition in 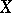: 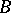is the boundary of 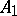, which is the boundary of 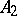, where 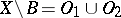, in which 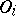is the open kernel (cf. Kernel of a set) of 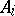, 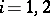. The converse is also true. In essence, the concept of a partition between sets leads to the concept of connectedness. The converse also applies: A space 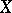is disconnected if 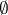is a partition between non-empty sets.

Comments

Related notions in this context are those of a separator and of a cut.

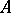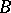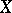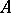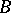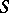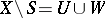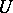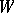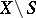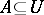If and are disjoint subsets of a space , then a separator between and is a set such that with and disjoint and open in , and and 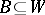. So a partition is a closed separator.

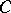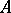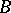A set is a cut between and if 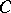intersects every continuum that intersects both 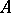and .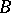

One readily sees that every partition is a separator and that every separator is a cut, and the following examples show that the notions are in general distinct: the open interval 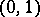is a separator between 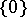and 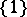in the interval 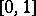, but not a partition; in the well-known subspace 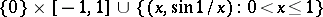of the Euclidean space, the point 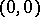is a cut but not a separator between the points 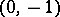and .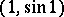

A partition of a positive integer is a decomposition of as a sum of positive integers. For example, the partitions of 4 read: 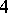, , 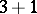, , 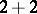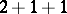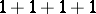. The number of different partitions of is denoted by 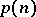. So, 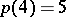. L. Euler gave a non-trivial recurrence relation for 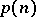(see [a1]) and Ramanujan discovered the surprising congruences 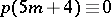(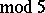), 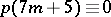(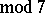), 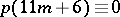(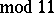), and others. He also found the asymptotic relation

where 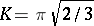. Later this was completed to an exact series expansion by H. Rademacher (see [a2]).

One can also distinguish other partitions, having particular properties, such as the numbers in the decomposition being distinct (see [a3]). See also Additive number theory; Additive problems.

References

[a1]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XVI
[a2]	T.M. Apostol, "Modular functions and Dirichlet series in number theory" , Springer (1976)
[a3]	G.E. Andrews, "The theory of partitions" , Addison-Wesley (1976)
[a4]	R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50