Dante space
From Encyclopedia of Mathematics
A type of topological space. Let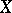 
be a topological space, let 
be a subspace of it and let 
and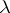 
be infinite cardinals. The space 
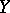is said to be 
-monolithic in 
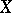if for each 
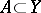such that 
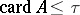the closure 
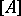in 
is a compactum of weight 
. The space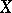 
-suppresses the subspace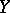 
if it follows from 
, 
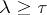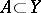and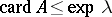 
that there exists an 
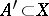for which 
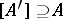and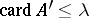 
. The space 
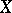is said to be a Dante space if for each infinite cardinal 
there exists an everywhere-dense subspace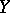 
in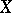 
which is both monolithic in itself and is 
-suppressed by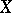 
. The class of Dante spaces contains the class of dyadic compacta (cf. Dyadic compactum).
Comments
For applications of these notions see [a1].
References
| [a1] | A.V. Arkhangel'skii, "Factorization theorems and spaces of continuous functions: stability and monolithicity" Sov. Math. Dokl. , 26 (1982) pp. 177–181 Dokl. Akad. Nauk SSSR , 265 : 5 (1982) pp. 1039–1043 |
How to Cite This Entry:
Dante space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dante_space&oldid=16209
Dante space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dante_space&oldid=16209
This article was adapted from an original article by B.A. Efimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article