Wiener-Itô decomposition
Itô–Wiener decomposition
An orthogonal decomposition of the Hilbert space of square-integrable functions on a Gaussian space. It was first proved in 1938 by N. Wiener [a6] in terms of homogeneous chaos (cf. also Wiener chaos decomposition). In 1951, K. Itô [a1] defined multiple Wiener integrals to interpret homogeneous chaos and gave a different proof of the decomposition theorem.
Take an abstract Wiener space 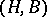 [a3] (cf. also Wiener space, abstract). Let
[a3] (cf. also Wiener space, abstract). Let 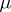 be the standard Gaussian measure on
be the standard Gaussian measure on 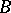 . The abstract version of Wiener–Itô decomposition deals with a special orthogonal decomposition of the real Hilbert space
. The abstract version of Wiener–Itô decomposition deals with a special orthogonal decomposition of the real Hilbert space 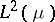 .
.
Each 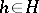 defines a normal random variable
defines a normal random variable 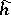 on
on 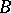 with mean
with mean  and variance
and variance 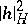 [a3]. Let
[a3]. Let 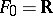 . For
. For 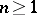 , let
, let 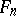 be the
be the 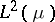 -closure of the linear space spanned by
-closure of the linear space spanned by 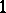 and random variables of the form
and random variables of the form 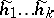 with
with 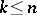 and
and  for
for 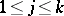 . Then
. Then 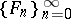 is an increasing sequence of closed subspaces of
is an increasing sequence of closed subspaces of 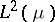 . Let
. Let  and, for
and, for 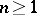 , let
, let  be the orthogonal complement of
be the orthogonal complement of 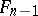 in
in  . The elements in
. The elements in 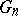 are called homogeneous chaos of degree
are called homogeneous chaos of degree  . Obviously, the spaces
. Obviously, the spaces 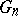 are orthogonal. Moreover, the Hilbert space
are orthogonal. Moreover, the Hilbert space 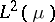 is the direct sum of
is the direct sum of 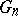 for
for 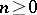 , namely,
, namely, 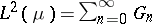 .
.
Fix 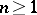 . To describe
. To describe 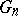 more precisely, let
more precisely, let 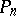 be the orthogonal projection of
be the orthogonal projection of 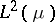 onto the space
onto the space  . For
. For 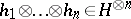 , define
, define
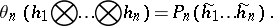 |
Then 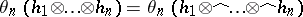 (where
(where 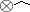 denotes the symmetric tensor product) and
denotes the symmetric tensor product) and
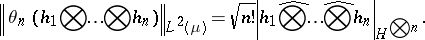 |
Thus,  extends by continuity to a continuous linear operator from
extends by continuity to a continuous linear operator from 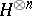 into
into 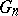 and is an isometric mapping (up to the constant
and is an isometric mapping (up to the constant 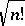 ) from
) from 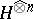 into
into 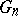 . Actually,
. Actually, 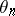 is surjective and so for any
is surjective and so for any 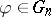 , there exists a unique
, there exists a unique 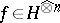 such that
such that 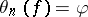 and
and 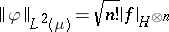 . Therefore, for any
. Therefore, for any 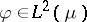 , there exists a unique sequence
, there exists a unique sequence 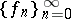 with
with 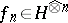 such that
such that
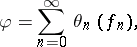 |
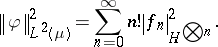 |
This is the abstract version of the Wiener–Itô decomposition theorem [a2], [a4], [a5].
Let 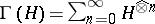 . Define a norm on
. Define a norm on 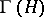 by
by
 |
The Hilbert space 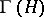 is called the Fock space of
is called the Fock space of 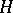 (cf. also Fock space). The spaces
(cf. also Fock space). The spaces 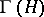 and
and 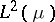 are isomorphic under the unitary operator
are isomorphic under the unitary operator 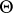 defined by
defined by
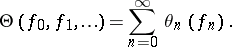 |
Let 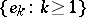 be an orthonormal basis (cf. also Orthogonal basis) for
be an orthonormal basis (cf. also Orthogonal basis) for 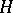 . For any non-negative integers
. For any non-negative integers 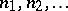 such that
such that 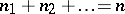 , define
, define
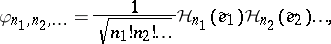 |
where 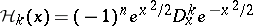 is the Hermite polynomial of degree
is the Hermite polynomial of degree 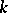 (cf. also Hermite polynomials). The set
(cf. also Hermite polynomials). The set 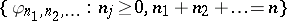 is an orthonormal basis for the space
is an orthonormal basis for the space  of homogeneous chaos of degree
of homogeneous chaos of degree  . Hence the set
. Hence the set 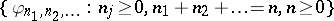 forms an orthonormal basis for
forms an orthonormal basis for 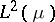 .
.
Consider the classical Wiener space 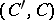 [a3]. The Hilbert space
[a3]. The Hilbert space 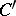 is isomorphic to
is isomorphic to 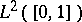 under the unitary operator
under the unitary operator 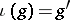 ,
, 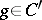 . The standard Gaussian measure
. The standard Gaussian measure 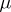 on
on 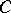 is the Wiener measure and
is the Wiener measure and 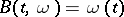 ,
, 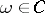 , is a Brownian motion. For
, is a Brownian motion. For 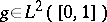 , the random variable
, the random variable 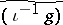 is exactly the Wiener integral
is exactly the Wiener integral 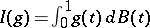 . Let
. Let 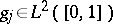 ,
, 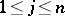 . The random variable
. The random variable
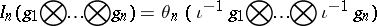 |
is a homogeneous chaos in the space 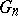 . The mapping
. The mapping 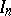 extends by continuity to the space
extends by continuity to the space 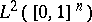 . For
. For 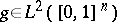 ,
,
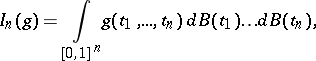 |
where the right-hand side is a multiple Wiener integral of order  as defined by Itô in [a1] and
as defined by Itô in [a1] and 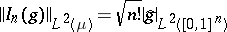 (where
(where 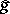 is the symmetrization of
is the symmetrization of 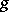 .) For any
.) For any 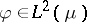 there exists a unique sequence
there exists a unique sequence 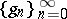 of symmetric functions
of symmetric functions 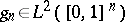 such that
such that
 |
 |
This is the Wiener–Itô decomposition theorem in terms of multiple Wiener integrals. An orthonormal basis for 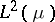 is given by the set
is given by the set
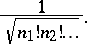 |
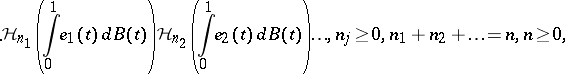 |
where 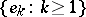 is an orthonormal basis for
is an orthonormal basis for 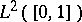 and the integrals are Wiener integrals.
and the integrals are Wiener integrals.
References
| [a1] | K. Itô, "Multiple Wiener integral" J. Math. Soc. Japan , 3 (1951) pp. 157–169 |
| [a2] | G. Kallianpur, "Stochastic filtering theory" , Springer (1980) |
| [a3] | H.-H. Kuo, "Gaussian measures in Banach spaces" , Lecture Notes in Mathematics , 463 , Springer (1975) |
| [a4] | H.-H. Kuo, "White noise distribution theory" , CRC (1996) |
| [a5] | N. Obata, "White noise calculus and Fock space" , Lecture Notes in Mathematics , 1577 , Springer (1994) |
| [a6] | N. Wiener, "The homogeneous chaos" Amer. J. Math. , 60 (1938) pp. 897–936 |
Wiener-Itô decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener-It%C3%B4_decomposition&oldid=16199