Complete set of functionals
From Encyclopedia of Mathematics
total set of functionals
A set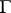 
of continuous linear functionals 
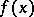, defined on a linear topological space 
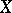, such that there is no element 
, 
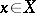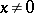, on which the equality 
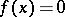is satisfied for all 
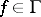. Every locally convex space has a complete set of functionals.
How to Cite This Entry:
Complete set of functionals. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_set_of_functionals&oldid=16190
Complete set of functionals. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_set_of_functionals&oldid=16190
This article was adapted from an original article by M.I. Kadets (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article