Jacobson-Bourbaki theorem
The Jacobson–Bourbaki theorem is especially useful for generalizations of the Galois theory of finite, normal and separable field extensions.
Let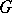 
be a finite group of automorphisms of a field 
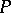, and let 
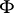be the subfield of elements of 
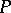that are invariant under the action of 
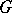. Then 
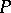is a normal and separable extension of 
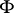(cf. Extension of a field), and there is a one-to-one correspondence between the subfields of 
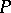containing 
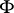and the subgroups of 
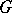(cf. also Galois theory). The elements of 
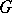are linear operators on the vector space 
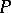over 
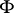; by the operation of multiplication, the elements of 
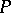can be represented as linear operators on 
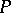over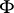 
(the regular representation), and the ring 
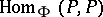of all linear operators on 
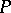over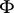 
is generated by 
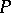and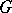 
; indeed, it is the cross product of 
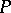and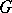 
.
Now, let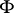 
be a subfield of 
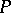such that 
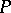is a finite-dimensional vector space over 
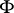and to each subfield 
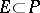containing 
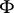let correspond the ring 
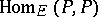of linear operators on the vector space 
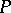over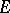 
. The Jacobson–Bourbaki theorem asserts that this correspondence is a bijection between the subfields of 
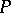containing 
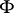and the set of subrings of 
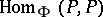that are left vector spaces over 
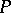of finite dimension. Moreover, the dimension of 
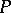over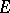 
equals the dimension of 
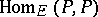over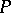 
.
This theorem has been used by N. Jacobson to develop a Galois theory of finite, purely inseparable field extensions of exponent one, in which groups of automorphisms are replaced by Lie algebras of derivations, [a1].
The Jacobson–Bourbaki theorem can be regarded as an instance of Morita duality. From the theory of Morita equivalence the following very general result is obtained. Let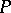 
be a ring, let 
be the ring of endomorphisms of the additive group of 
an note that 
is a left module over 
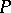. There is a one-to-one correspondence between those subrings 
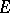of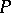 
such that 
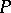is a finitely generated projective generator in the category of right 
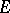-modules and the subrings 
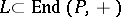such that 
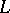is a submodule of the left 
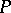-module 
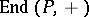and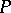 
is a finitely generated projective generator in the category of left 
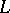-modules.
References
| [a1] | N. Jacobson, "Galois theory of purely inseparable fields of exponent one" Amer. J. Math. , 66 (1944) pp. 645–648 |
Jacobson-Bourbaki theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobson-Bourbaki_theorem&oldid=16163