Cyclotomic polynomials
circular polynomials
The polynomials  that satisfy the relation
that satisfy the relation
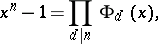 |
where the product is taken over all positive divisors  of the number
of the number  , including
, including  itself. Over the field of complex numbers one has
itself. Over the field of complex numbers one has
 |
where  ranges over the primitive
ranges over the primitive  -th roots of unity (cf. Primitive root). The degree of
-th roots of unity (cf. Primitive root). The degree of  is the number of integers
is the number of integers  among
among  that are relatively prime with
that are relatively prime with  . The polynomials
. The polynomials 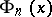 can be computed recursively by dividing the polynomial
can be computed recursively by dividing the polynomial 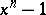 by the product of all
by the product of all  ,
, 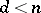 ,
, 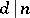 . The coefficients lie in the prime field
. The coefficients lie in the prime field 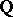 ; in case of characteristic zero, they are integers. Thus,
; in case of characteristic zero, they are integers. Thus,
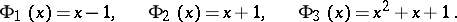 |
If, moreover, 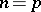 is prime, then
is prime, then
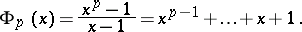 |
The polynomial  can be explicitly expressed using the Möbius function
can be explicitly expressed using the Möbius function 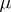 :
:
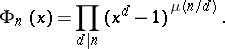 |
For example,
 |
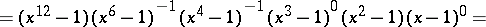 |
 |
All the polynomials  are irreducible over the field of rational numbers, but they may be reducible over finite prime fields. Thus, the relation
are irreducible over the field of rational numbers, but they may be reducible over finite prime fields. Thus, the relation
 |
is valid over the field of residues modulo 11.
The equation  , which gives all primitive
, which gives all primitive  -th roots of unity, is known as the equation of division of the circle. The solution of this equation in trigonometric form is
-th roots of unity, is known as the equation of division of the circle. The solution of this equation in trigonometric form is
 |
where the fraction 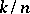 is irreducible, i.e.
is irreducible, i.e.  and
and  are relatively prime. The solution of the equation of division of the circle by radicals is closely connected with the problem of constructing a regular
are relatively prime. The solution of the equation of division of the circle by radicals is closely connected with the problem of constructing a regular  -gon, or with the equivalent problem of subdividing the circle into
-gon, or with the equivalent problem of subdividing the circle into  equal parts; the latter problem can be solved using a straightedge and a pair of compasses if and only if the equation
equal parts; the latter problem can be solved using a straightedge and a pair of compasses if and only if the equation 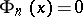 is solvable in quadratic radicals. It was shown by C.F. Gauss in 1801 that this condition is satisfied if and only if
is solvable in quadratic radicals. It was shown by C.F. Gauss in 1801 that this condition is satisfied if and only if
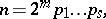 |
where  is a non-negative integer and
is a non-negative integer and  are pairwise different prime numbers of the form
are pairwise different prime numbers of the form 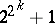 , where
, where  is a non-negative integer.
is a non-negative integer.
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | A.K. Sushkevich, "Foundations of higher algebra" , Moscow-Leningrad (1941) (In Russian) |
Comments
The degree of  is equal to
is equal to  , the value (at
, the value (at  ) of the Euler
) of the Euler 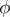 -function (cf. Euler function).
-function (cf. Euler function).
Prime numbers of the form  with
with  a non-negative integer are called Fermat primes, these numbers are related to a problem of Fermat: When is the number
a non-negative integer are called Fermat primes, these numbers are related to a problem of Fermat: When is the number  , with
, with 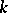 as before, prime? The only small Fermat primes are
as before, prime? The only small Fermat primes are  ,
, 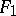 ,
, 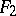 ,
,  ,
,  (cf. [a1], pp. 183-185).
(cf. [a1], pp. 183-185).
References
| [a1] | I. Stewart, "Galois theory" , Chapman & Hall (1973) |
| [a2] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
Cyclotomic polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cyclotomic_polynomials&oldid=16160