G-fibration
fibre bundle with a structure group
A generalization of the concept of the direct product of two topological spaces.
Let 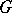 be a topological group and
be a topological group and  an effective right
an effective right 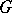 -space, i.e. a topological space with a given right action of
-space, i.e. a topological space with a given right action of 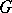 such that
such that 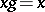 for some
for some 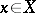 ,
, 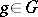 , implies
, implies 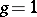 . Let
. Let 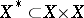 be the subset of those pairs
be the subset of those pairs 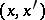 for which
for which 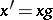 for some
for some 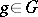 , let
, let 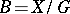 be the orbit space, and let
be the orbit space, and let  be the mapping sending each point to its orbit. If the mapping
be the mapping sending each point to its orbit. If the mapping 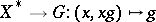 is continuous, then the tuple
is continuous, then the tuple 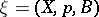 is called a principal fibre bundle with structure group
is called a principal fibre bundle with structure group 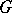 .
.
Let 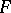 be a left
be a left 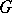 -space. The topological space
-space. The topological space 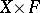 admits a right action of
admits a right action of 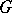 by
by 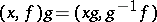 ,
, 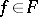 . The composition
. The composition 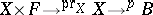 induces a mapping:
induces a mapping: 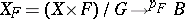 (where
(where 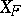 is the orbit space of
is the orbit space of 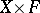 under the action of
under the action of 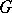 ). The quadruple
). The quadruple 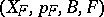 is called a fibre bundle with structure group associated with the principal fibre bundle
is called a fibre bundle with structure group associated with the principal fibre bundle 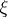 , and the quadruple
, and the quadruple 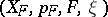 is a fibre bundle with fibre
is a fibre bundle with fibre 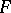 , base
, base  and structure group
and structure group 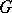 . Thus, a principal fibre bundle with a given structure group is a part of the structure of any fibre bundle with (that) structure group, and it uniquely determines the fibre bundle for any left
. Thus, a principal fibre bundle with a given structure group is a part of the structure of any fibre bundle with (that) structure group, and it uniquely determines the fibre bundle for any left 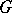 -space
-space 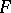 .
.
If 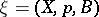 ,
,  are two principal fibre bundles with structure group
are two principal fibre bundles with structure group 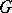 , then a morphism
, then a morphism  is a mapping of
is a mapping of 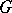 -spaces
-spaces 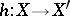 .
. 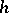 induces a mapping
induces a mapping 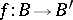 . A principal fibre bundle with structure group is called trivial is it is isomorphic to a fibre bundle of the following type:
. A principal fibre bundle with structure group is called trivial is it is isomorphic to a fibre bundle of the following type:
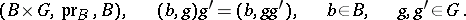 |
Let 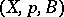 be a principal fibre bundle and let
be a principal fibre bundle and let 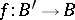 be a continuous mapping of an arbitrary topological space
be a continuous mapping of an arbitrary topological space 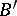 into
into 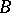 . Let
. Let 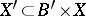 be the subset of pairs
be the subset of pairs 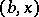 for which
for which 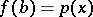 . The projection
. The projection 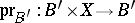 induces a mapping
induces a mapping 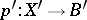 . The space
. The space 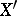 has the natural structure of a right
has the natural structure of a right 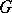 -space, and the triple
-space, and the triple 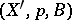 is a principal fibre bundle; it is induced by
is a principal fibre bundle; it is induced by 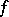 and is called an induced fibre bundle. If
and is called an induced fibre bundle. If 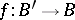 is the inclusion mapping of a subspace, then
is the inclusion mapping of a subspace, then 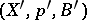 is called the restriction of
is called the restriction of 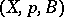 over the subspace
over the subspace 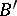 .
.
A principal fibre bundle with structure group is called locally trivial if its restriction to some neighbourhood of any point of the base 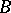 is trivial. For a wide class of cases, the requirement of local triviality is unnecessary (e.g. if
is trivial. For a wide class of cases, the requirement of local triviality is unnecessary (e.g. if 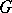 is a compact Lie group and
is a compact Lie group and 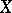 a smooth
a smooth  -manifold). Hence, the term "fibre bundle" with structure group is often used in the sense of a locally trivial fibre bundle (or fibration).
-manifold). Hence, the term "fibre bundle" with structure group is often used in the sense of a locally trivial fibre bundle (or fibration).
Let 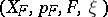 ,
, 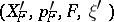 be a pair of fibre bundles with the same structure group and the same
be a pair of fibre bundles with the same structure group and the same 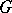 -space as fibre. Given a morphism
-space as fibre. Given a morphism 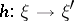 of principal fibre bundles, the mapping
of principal fibre bundles, the mapping 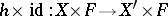 induces a continuous mapping
induces a continuous mapping 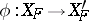 , and the pair
, and the pair 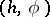 is called a morphism of fibre bundles with structure group,
is called a morphism of fibre bundles with structure group, 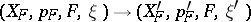 .
.
A locally trivial fibre bundle 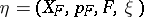 admits the following characterization, which gives rise to another (also generally accepted) definition of a fibre bundle with structure group. Let
admits the following characterization, which gives rise to another (also generally accepted) definition of a fibre bundle with structure group. Let 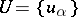 be an open covering of the base
be an open covering of the base 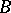 such that the restriction of
such that the restriction of 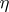 to
to  is trivial for all
is trivial for all 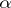 . The choice of trivializations and their equality on the intersections
. The choice of trivializations and their equality on the intersections 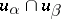 leads to continuous functions (called transfer functions)
leads to continuous functions (called transfer functions) 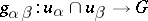 . On the intersection of three neighbourhoods
. On the intersection of three neighbourhoods 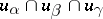 one has
one has 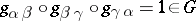 , while the choice of other trivializations over every neighbourhood leads to new functions
, while the choice of other trivializations over every neighbourhood leads to new functions 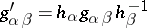 . In this way, the functions
. In this way, the functions 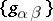 form a one-dimensional Aleksandrov–Čech cocycle with coefficients in the sheaf of germs of
form a one-dimensional Aleksandrov–Čech cocycle with coefficients in the sheaf of germs of 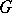 -valued functions (the coefficients are non-Abelian), and a locally trivial fibre bundle determines this cocycle up to a coboundary.
-valued functions (the coefficients are non-Abelian), and a locally trivial fibre bundle determines this cocycle up to a coboundary.
References
| [1] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [2] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
G-fibration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G-fibration&oldid=16144