Suspension
of a topological space (CW-complex) 
The space (CW-complex)
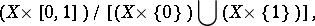 |
where  is the unit interval and the slant line denotes the operation of identifying a subspace with one point. The suspension of a pointed space
is the unit interval and the slant line denotes the operation of identifying a subspace with one point. The suspension of a pointed space  is defined to be the pointed space
is defined to be the pointed space
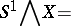 |
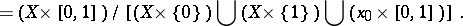 |
This is also known as a reduced or contracted suspension. A suspension is denoted by  (or sometimes
(or sometimes  ). The correspondence
). The correspondence  defines a functor from the category of topological (pointed) spaces into itself.
defines a functor from the category of topological (pointed) spaces into itself.
Since the suspension operation is a functor, one can define a homomorphism 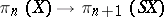 , which is also called the suspension. This homomorphism is identical with the composite of the homomorphism induced by the imbedding
, which is also called the suspension. This homomorphism is identical with the composite of the homomorphism induced by the imbedding  and the Hurewicz isomorphism
and the Hurewicz isomorphism 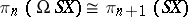 , where
, where  is the operation of forming loop spaces (cf. Loop space). For any homology theory
is the operation of forming loop spaces (cf. Loop space). For any homology theory 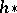 (cohomology theory
(cohomology theory  ) one has an isomorphism
) one has an isomorphism
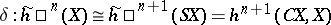 |
that coincides with the connecting homomorphism of the exact sequence of the pair 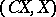 , where
, where  is the cone over
is the cone over  . The image of a class
. The image of a class  under this isomorphism is known as the suspension of
under this isomorphism is known as the suspension of  and is denoted by
and is denoted by  (or
(or 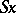 ).
).
The suspension of a cohomology operation  is defined to be the cohomology operation whose action on
is defined to be the cohomology operation whose action on  coincides with
coincides with  , and whose action on
, and whose action on  coincides with that of
coincides with that of  .
.
Comments
The suspension functor and the loop space functor on the category of pointed spaces are adjoint:
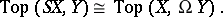 |
The bijection above associates to  the mapping
the mapping 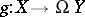 which associates the loop
which associates the loop  to
to 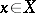 . This adjointness is compatible with the homology and thus also defines an adjunction for the category of pointed topological spaces and homotopy classes of mappings.
. This adjointness is compatible with the homology and thus also defines an adjunction for the category of pointed topological spaces and homotopy classes of mappings.
References
| [a1] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. Chapt. 2 |
Suspension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Suspension&oldid=16128