Motives, theory of

A generalization of the various cohomology theories of algebraic varieties. The theory of motives systematically generalizes the idea of using the Jacobian of an algebraic curve 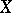as a replacement for the cohomology group in the classical theory of correspondences, and the use of this theory in the study of the zeta-function of a curve over a finite field. The theory of motives is universal in the sense that every geometric cohomology theory, of the type of the classical singular cohomology for algebraic varieties over 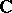with constant coefficients, every -adic cohomology theory for various prime numbers 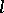different from the characteristic of the ground field, every crystalline cohomology theory, etc. (see Weil cohomology) are functors on the category of motives.

Let 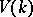be the category of smooth projective varieties over a field and let 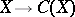be a contravariant functor of global intersection theory from 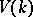into the category of commutative 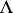-algebras, where 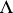is a fixed ring. For example, 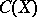is the Chow ring of classes of algebraic cycles (cf. Algebraic cycle) on modulo a suitable (rational, algebraic, numerical, etc.) equivalence relation, or 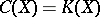is the Grothendieck ring, or 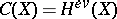is the ring of cohomology classes of even dimension, etc. The category 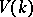and the functor 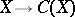enable one to define a new category, the category of correspondences 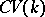, whose objects are varieties 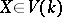, denoted by 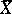, and whose morphisms are defined by the formula

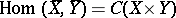with the usual composition law for correspondences (see [1]). Let the functor 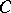take values in the category of commutative graded 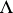-algebras 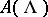. Then 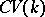will be the -additive category of graded correspondences. Moreover, 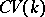will have direct sums and tensor products.

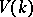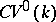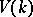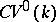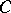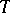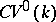The category whose objects are the varieties from and whose morphisms are correspondences of degree is denoted by . A natural functor from into has been defined, and the functor extends to a functor from to 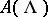. The category 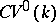, like 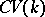, is not Abelian. Its pseudo-Abelian completion, the category 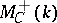, has been considered. It is obtained from 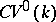by the formal addition of the images of all projections 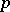. 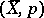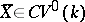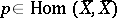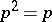More precisely, the objects of are pairs , where and , , and 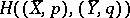is the set of correspondences 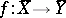such that 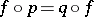modulo a correspondence 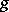with 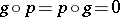. The category 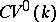is imbedded in 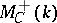by means of the functor 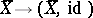. The natural functor 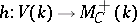is called the functor of motive cohomology spaces and 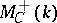is called the category of effective motives.

Let 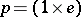, where is the class of any rational point on the projective line 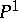, and let . Then

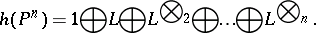If 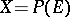is the projectivization of a locally free sheaf 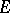of rank on 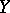, then

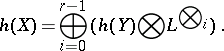Motives of a monodial transformation with a non-singular centre, motives of curves (see [1]), motives of Abelian manifolds (see [2]), and motives of Weil hypersurfaces have also been calculated.

The category of motives 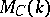is obtained from 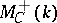by the formal addition of negative powers of the motives 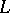. By analogy with 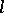-adic cohomology, 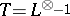is called the Tate motive. Tensor multiplication with 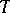is called twisting by the Tate motive. Twisting enables one to define the level of a motive as in an 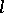-adic cohomology theory. Any functor of the Weil cohomology factors through the functor 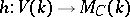. There is the conjecture that 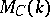does not, in some sense, depend on the intersection theory of 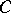, and that the functor 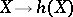is itself a (universal) theory for the Weil cohomology. This conjecture is closely related to the standard Grothendieck conjectures (see [5]) on algebraic cycles (at present, 1982, not proved).

References

[1]	Yu.I. Manin, "Correspondences, motives and monoidal transformations" Math. USSR Sb. , 6 : 4 (1968) pp. 439–470 Mat. Sb. , 77 : 4 (1968) pp. 475–507
[2]	A.M. Shermenev, "The motif of an abelian variety" Uspekhi Mat. Nauk , 26 : 2 (1971) pp. 215–216 (In Russian)
[3]	M. Demazure, "Motives des variétés algébrique" , Sem. Bourbaki Exp. 365 , Lect. notes in math. , 180 , Springer (1971) pp. 19–38
[4]	S.L. Kleiman, "Motives" P. Holm (ed.) , Algebraic Geom. Proc. 5-th Nordic Summer School Math. Oslo, 1970 , Wolters-Noordhoff (1972) pp. 53–96
[5]	S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386

Comments

The theory of motives has been created by A. Grothendieck in the 1960-s. Although the above-mentioned standard conjectures on algebraic cycles have not yet (1989) been proved, the theory of motives has played an important role in various recent developments, for instance: i) as a guide for the Deligne–Hodge theory ([a1]); ii) in the study of absolute Hodge cycles on Abelian varieties ([a2]), where a variant of the notion of a motive has been used; iii) in the study of Chow groups on certain varieties over a finite field ([a3]); and iv) in work on the Beilinson's conjectures on special values of 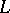-functions (see [a4]).

References

[a1]	P. Deligne, "Theory de Hodge I" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 425–430
[a2]	P. Deligne (ed.) J.S. Milne (ed.) A. Ogus (ed.) K. Shih (ed.) , Hodge cycles, motives and Shimura varieties , Lect. notes in math. , 900 , Springer (1980)
[a3]	C. Soulé, "Groupes de Chow et 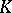-theory des variétés sur un corps fini" Math. Ann. , 268 (1984) pp. 317–345
[a4]	M. Rapoport (ed.) N. Schappacher (ed.) P. Schneider (ed.) , Beilinson's conjectures on special values of 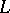-functions , Acad. Press (1988)