Interior mapping
A mapping 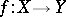 from a topological space
from a topological space 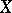 into a topological space
into a topological space 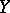 such that the image of any set
such that the image of any set 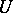 open in
open in 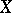 is also open in
is also open in 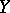 , while the inverse image
, while the inverse image 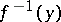 of any point
of any point 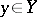 is totally disconnected (i.e. does not contain connected components other than points).
is totally disconnected (i.e. does not contain connected components other than points).
Let 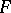 map some Riemann surface
map some Riemann surface 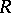 into the sphere
into the sphere 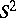 ; a homeomorphism
; a homeomorphism 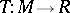 from an oriented surface
from an oriented surface 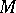 will then induce a mapping
will then induce a mapping
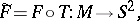 |
which is topologically equivalent with 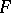 . For an analytic function
. For an analytic function 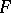 and some mapping
and some mapping 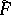 to be topologically equivalent it is necessary and sufficient for
to be topologically equivalent it is necessary and sufficient for 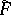 to be an interior mapping (then there exists a homeomorphism
to be an interior mapping (then there exists a homeomorphism 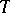 such that
such that 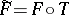 ) (Stoilow's theorem).
) (Stoilow's theorem).
The local structure of the interior mapping 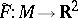 may be described as follows. For any point
may be described as follows. For any point 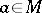 there exist a neighbourhood
there exist a neighbourhood 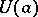 and homeomorphisms
and homeomorphisms 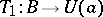 of the unit disc
of the unit disc 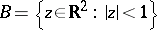 onto
onto 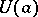 and
and 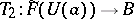 such that
such that 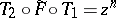 .
.
References
| [1] | S. [S. Stoilov] Stoilow, "Leçons sur les principes topologiques de la théorie des fonctions analytiques" , Gauthier-Villars (1938) |
Comments
References
| [a1] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [a2] | G.T. Whyburn, "Topological analysis" , Princeton Univ. Press (1964) |
Interior mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Interior_mapping&oldid=16109