Steenrod problem

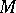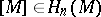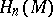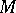The problem of the realization of cycles (homology classes) by singular manifolds; formulated by N. Steenrod, cf. [1]. Let be a closed oriented manifold (topological, piecewise-linear, smooth, etc.) and let be its orientation (here is the -dimensional homology group of ). Any continuous mapping 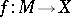defines an element 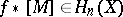. The Steenrod problem consists of describing those homology classes of 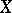, called realizable, which are obtained in this way, i.e. which take the form 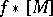for a certain 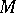from the given class. All elements of the groups 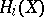, , 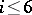are realizable by a smooth manifold. Any element of the group 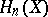, , 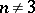is realizable by a mapping of a Poincaré complex 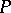. Moreover, any cycle can be realized by a pseudo-manifold. Non-orientable manifolds can also be considered, and every homology class modulo (i.e. element of 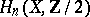) can be realized by a non-oriented smooth singular manifold .

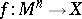Thus, for smooth 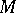the Steenrod problem consists of describing the form of the homomorphism 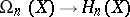, where 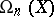is the oriented bordism group of the space. The connection between the bordisms 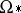and the Thom spaces (cf. Thom space) 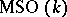, discovered by R. Thom [2], clarified the Steenrod problem by reducing it to the study of the mappings 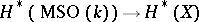. A non-realizable class 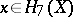has been exhibited, where is the Eilenberg–MacLane space 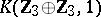. 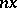For any class , some multiple is realizable (by a smooth manifold); moreover, can be chosen odd.

References

[1]	S. Eilenberg, "On the problems of topology" Ann. of Math. , 50 (1949) pp. 247–260
[2]	R. Thom, "Quelques propriétés globales des variétés differentiables" Comm. Math. Helv. , 28 (1954) pp. 17–86
[3]	P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964)
[4]	R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968)
[5]	Yu.B. Rudyak, "Realization of homology classes of PL-manifolds with singularities" Math. Notes , 41 : 5 (1987) pp. 417–421 Mat. Zametki , 41 : 5 (1987) pp. 741–749