Nilpotent element

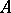An element of a ring or semi-group with zero such that for some natural number . The smallest such is called the nilpotency index of . For example, in the residue ring modulo 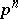(under multiplication), where is a prime number, the residue class of 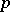is nilpotent of index ; in the ring of 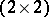-matrices with coefficients in a field 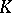the matrix

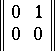is nilpotent of index 2; in the group algebra 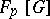, where 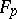is the field with 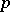elements and 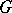the cyclic group of order 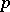generated by 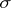, the element 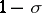is nilpotent of index .

If is a nilpotent element of index , then

that is, 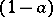is invertible in 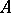and its inverse can be written as a polynomial in .

In a commutative ring 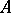an element is nilpotent if and only if it is contained in all prime ideals of the ring. All nilpotent elements form an ideal 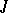, the so-called nil radical of the ring; it coincides with the intersection of all prime ideals of 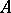. The ring 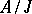has no non-zero nilpotent elements.

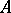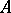In the interpretation of a commutative ring as the ring of functions on the space (the spectrum of , cf. Spectrum of a ring), the nilpotent elements correspond to functions that vanish identically. Nevertheless, the consideration of nilpotent elements frequently turns out to be useful in algebraic geometry because it makes it possible to obtain purely algebraic analogues of a number of concepts in analysis and differential geometry (infinitesimal deformations, etc.).

References

[1]	S. Lang, "Algebra" , Addison-Wesley (1974)
[2]	I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968)
[3]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)

Comments

An element of an associative ring 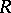is strongly nilpotent if every sequence such that is ultimately zero. Obviously, every strongly-nilpotent element is nilpotent. The prime radical of a ring 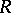, i.e. the intersection of all prime ideals, consists of precisely the strongly-nilpotent elements. It is a nil ideal.

References

[a1]	J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) pp. §0.2