Uniform distribution
A common name for a class of probability distributions, arising as an extension of the idea of "equally possible outcomes" to the continuous case. As with the normal distribution, the uniform distribution appears in probability theory as an exact distribution in some problems and as a limit in others.
The uniform distribution on an interval of the line (the rectangular distribution).
The uniform distribution on an interval 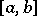 ,
, 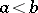 , is the probability distribution with density
, is the probability distribution with density
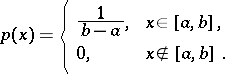 |
The concept of a uniform distribution on 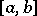 corresponds to the representation of a random choice of a point from the interval. The mathematical expectation and variance of the uniform distribution are equal, respectively, to
corresponds to the representation of a random choice of a point from the interval. The mathematical expectation and variance of the uniform distribution are equal, respectively, to 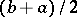 and
and 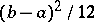 . The distribution function is
. The distribution function is
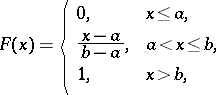 |
and the characteristic function is
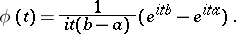 |
A random variable with uniform distribution on 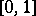 can be constructed from a sequence of independent random variables
can be constructed from a sequence of independent random variables 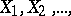 taking the values 0 and 1 with probabilities
taking the values 0 and 1 with probabilities 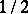 , by putting
, by putting
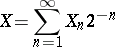 |
(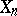 are the digits in the binary expansion of
are the digits in the binary expansion of  ). The random number
). The random number 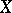 has a uniform distribution in the interval
has a uniform distribution in the interval 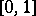 . This fact has important statistical applications, see, for example, Random and pseudo-random numbers.
. This fact has important statistical applications, see, for example, Random and pseudo-random numbers.
If two independent random variables 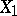 and
and 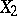 have uniform distributions on
have uniform distributions on 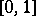 , then their sum has the so-called triangular distribution on
, then their sum has the so-called triangular distribution on 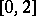 with density
with density 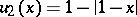 for
for 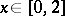 and
and 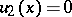 for
for 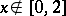 . The sum of three independent random variables with uniform distributions on
. The sum of three independent random variables with uniform distributions on 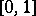 has on
has on 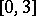 the distribution with density
the distribution with density
 |
In general, the distribution of the sum 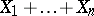 of independent variables with uniform distributions on
of independent variables with uniform distributions on 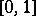 has density
has density
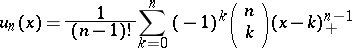 |
for  and
and 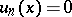 for
for 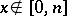 ; here
; here
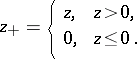 |
As 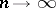 , the distribution of the sum
, the distribution of the sum 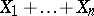 , centred around the mathematical expectation
, centred around the mathematical expectation 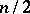 and scaled by the standard deviation
and scaled by the standard deviation 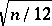 , tends to the normal distribution with parameters 0 and 1 (the approximation for
, tends to the normal distribution with parameters 0 and 1 (the approximation for 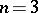 is already satisfactory for many practical purposes).
is already satisfactory for many practical purposes).
In statistical applications the procedure for constructing a random variable 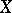 with given distribution function
with given distribution function  is based on the following fact. Let the random variable
is based on the following fact. Let the random variable  be uniformly distributed on
be uniformly distributed on 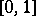 and let the distribution function
and let the distribution function 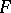 be continuous and strictly increasing. Then the random variable
be continuous and strictly increasing. Then the random variable 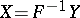 has distribution function
has distribution function 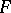 (in the general case it is necessary to replace the inverse function
(in the general case it is necessary to replace the inverse function 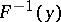 in the definition of
in the definition of 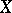 by an analogue, namely
by an analogue, namely 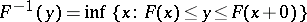 ).
).
The uniform distribution on an interval as a limit distribution.
Some typical examples of the uniform distribution on 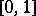 arising as a limit are given below.
arising as a limit are given below.
1) Let 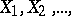 be independent random variables having the same continuous distribution function. Then the distribution of their sums
be independent random variables having the same continuous distribution function. Then the distribution of their sums 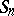 , taken
, taken 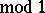 , that is, the distribution of the fractional parts
, that is, the distribution of the fractional parts 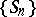 of these sums
of these sums 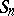 , converges to the uniform distribution on
, converges to the uniform distribution on 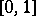 .
.
2) Let the random parameters 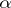 and
and 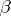 have an absolutely-continuous joint distribution; then, as
have an absolutely-continuous joint distribution; then, as 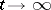 , the distribution of
, the distribution of 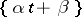 converges to the uniform distribution on
converges to the uniform distribution on 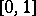 .
.
3) A uniform distribution appears as the limit distribution of the fractional parts of certain functions 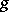 on the positive integers. For example, for irrational
on the positive integers. For example, for irrational 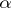 the fraction of those
the fraction of those 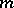 ,
, 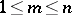 , for which
, for which
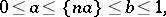 |
has the limit 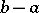 as
as 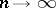 .
.
The uniform distribution on subsets of 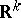 .
.
An example of a uniform distribution in a rectangle appears already in the Buffon problem (see also Geometric probabilities; Stochastic geometry). The uniform distribution on a bounded set 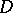 in
in 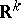 is defined as the distribution with density
is defined as the distribution with density
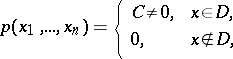 |
where 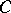 is the inverse of the
is the inverse of the 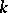 -dimensional volume (or Lebesgue measure) of
-dimensional volume (or Lebesgue measure) of 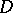 .
.
Uniform distributions on surfaces have also been discussed. Thus, a "random direction" (for example, in 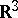 ), defined as a vector from the origin to a random point on the surface of the unit sphere, is uniformly distributed in the sense that the probability that it hits a part of the surface is proportional to the area of that part.
), defined as a vector from the origin to a random point on the surface of the unit sphere, is uniformly distributed in the sense that the probability that it hits a part of the surface is proportional to the area of that part.
The role of the uniform distribution in algebraic groups is played by the normalized Haar measure.
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1971) |
Uniform distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniform_distribution&oldid=16025