Bredon cohomology

An ordinary equivariant cohomology for a finite group , defined in [a1], on the category -CW of -complexes (cf. Complex; CW-complex). The objects of -CW are the CW-complexes with a cellular action of , satisfying the condition that, for every subgroup of , the fixed point set is a subcomplex of . The morphisms are the cellular 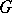-mappings. Let be the full subcategory of -CW whose objects are the -orbits 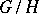, where is a subgroup of . 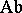For every contravariant functor from to the category of Abelian groups, there exists a Bredon cohomology theory which, after restriction to 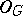, vanishes for and is equal to for .

Let 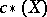be the chain complex of functors from to 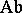such that, for every subgroup of , is the ordinary cellular chain complex of 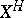. Then

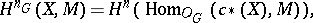where denotes the set of natural transformations of functors. The functors are projective objects in the category of coefficient systems and there is a spectral sequence

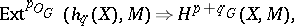where .

Let be a -space with base point (cf., e.g., Equivariant cohomology). Important examples of coefficient systems are the homotopy group functors defined by . The obstruction theory for 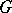-mappings is formulated in terms of the cohomology groups . For any coefficient system and natural number , there is a pointed Eilenberg–MacLane -complex 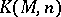such that 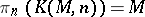and vanishes whenever . 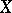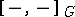For every -complex , , where denotes -homotopy classes of -mappings.

If 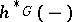is an equivariant cohomology theory defined on the category -CW, then there exists an Atiyah–Hirzebruch-type spectral sequence

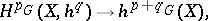where 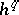is the restriction of to . Bredon cohomology for an arbitrary topological group is studied in [a4] and [a5]. Singular ordinary equivariant cohomology is defined in [a2] (the finite case) and in [a3]. If a coefficient system is a Mackey functor, then the Bredon cohomology can be extended to an ordinary -graded cohomology [a6].

References

[a1]	G.E. Bredon, "Equivariant cohomology theories" , Lecture Notes in Mathematics , 34 , Springer (1967)
[a2]	T. Bröcker, "Singuläre Definition der äquivarianten Bredon Homologie" Manuscr. Math. , 5 (1971) pp. 91–102
[a3]	S. Illman, "Equivariant singular homology and cohomology" , Memoirs , 156 , Amer. Math. Soc. (1975)
[a4]	T. Matumoto, "Equivariant cohomology theories on 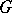-CW-complexes" Osaka J. Math. , 10 (1973) pp. 51–68
[a5]	S.J. Wilson, "Equivariant homology theories on 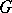-complexes" Trans. Amer. Math. Soc. , 212 (1975) pp. 155–171
[a6]	L.G. Lewis, J.P. May, J. McClure, "Ordinary RO(G)-graded cohomology" Bull. Amer. Math. Soc. , 4 (1981) pp. 208–212